পাইথনে সমান দূরত্বে আইটেম সংগ্রহ করতে কভার করা দূরত্ব খুঁজুন

ধরুন একটি রেস সংগঠিত হতে চলেছে৷ যেখানে একটি রাস্তার ওপর বিভিন্ন পাথর বসানো হয়েছে। রেসের শুরুতে একটি বালতি উপস্থিত রয়েছে, এটি প্রথম পাথর থেকে 6 ইউনিট দূরে। অন্য পাথরগুলো একে অপরের থেকে 4 একক দূরে এবং একের পর এক লাইনে সোজা হয়ে পড়ে আছে। এখন, অংশগ্রহণকারীরা বালতি থেকে শুরু করে, তারপর নিকটতম পাথরটি সংগ্রহ করে, ফিরে আসে এবং সেই পাথরটিকে বালতিতে রাখে, তারপরে পরবর্তী নিকটতম পাথরটি সংগ্রহ করতে আবার দৌড়ে, পিছনে দৌড়ে এবং বালতিতে রাখে। সমস্ত পাথর বালতিতে রাখা না হওয়া পর্যন্ত এই প্রক্রিয়াটি অব্যাহত থাকবে। যদি n পাথর থাকে, তাহলে আমাদের মোট দূরত্ব খুঁজে বের করতে হবে যা অংশগ্রহণকারীদের জন্য কভার করতে হবে।

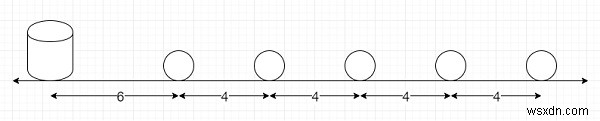
সুতরাং, যদি ইনপুটটি n =5 এর মত হয়, তাহলে আউটপুট 140 হবে 2*6 + 2(6 + 4) + 2(6 + 4 + 4) + 2(6 + 4 + 4 + 4) + 2 (6 + 4 + 4 + 4 + 4) =140

এটি সমাধান করতে, আমাদের এই সমীকরণটি সমাধান করতে হবে −

পাথর 1 এর জন্য, আমাদের (6+6) =2*6 দূরত্ব
কভার করতে হবে
পাথর 2-এর জন্য, আমাদেরকে ((6+4)+(6+4)) =2*(6+4) দূরত্ব কভার করতে হবে
পাথর 3-এর জন্য, আমাদেরকে (6+4+4)+(6+4+4)) =2*(6+4+4) দূরত্ব কভার করতে হবে
স্টোন n এর জন্য, আমাদেরকে ((6+4*(n-1))+(6+4*(n-1))) =2*(6+4*(n-1)) দূরত্ব কভার করতে হবে। পি>

সমস্ত পাথরের জন্য আমাদের আবরণ করতে হবে -

D =2*6 + 2*(6+4) + 2*(6+4+4) + … + 2*(6+4*(n-1))
D =2*[6 + (6+4) + (6+2*4) + … + (6+(n-1)*4)]
D =2*[6n + 4(1 + 2 + … + (n-1))]
D =2*[6n + 4(n*(n-1)/2)]
D =2*[6n + 2(n*(n-1))]

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def find_distance(n):
   return 2*(6*n + 2*((n-1)*n))
n = 5
print(find_distance(n))