ধরুন আমাদের একটি N x N বাইনারি ম্যাট্রিক্স আছে যেখানে 0 হল খালি কোষের জন্য এবং 1 হল একটি ব্লক করা কোষ, আমাদেরকে N খালি ঘরগুলি বেছে নেওয়ার উপায়গুলি খুঁজে বের করতে হবে যাতে প্রতিটি সারি এবং প্রতিটি কলামে কমপক্ষে একটি নির্বাচিত কোষ থাকে। উত্তরটি খুব বড় হলে রিটার্ন ফলাফল মোড 10^9 + 7
সুতরাং, যদি ইনপুট মত হয়
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
তাহলে আউটপুট হবে 4, যেমন আমাদের নিম্নলিখিত কনফিগারেশন রয়েছে (যেখানে x একটি নির্বাচিত সেল) -
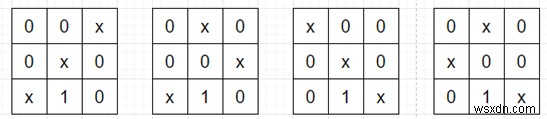
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- n :=ম্যাট্রিক্সের আকার
- একটি ফাংশন সংজ্ঞায়িত করুন f()। এর জন্য i, bs লাগবে
- যদি i>=n, তাহলে
- প্রত্যাবর্তন 1
- উত্তর :=0 0 থেকে n রেঞ্জের মধ্যে j-এর জন্য
- করুন
- যদি ম্যাট্রিক্স[i, j] 0 এবং (2^j এবং bs 0 এর সমান) হয়, তাহলে
- উত্তর :=ans + f(i + 1, bs OR 2^j)
- যদি ম্যাট্রিক্স[i, j] 0 এবং (2^j এবং bs 0 এর সমান) হয়, তাহলে
- উত্তর ফেরত দিন
- মূল পদ্ধতি থেকে কল করুন এবং f(0, 0) ফেরত দিন
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
উদাহরণ
class Solution: def solve(self, matrix): n = len(matrix) def f(i, bs): if i >= n: return 1 ans = 0 for j in range(n): if matrix[i][j] == 0 and ((1 << j) & bs == 0): ans += f(i + 1, bs | (1 << j)) return ans return f(0, 0) ob = Solution() matrix = [ [0, 0, 0], [0, 0, 0], [0, 1, 0] ] print(ob.solve(matrix))
ইনপুট
[ [0, 0, 0], [0, 0, 0], [0, 1, 0] ]
আউটপুট
4


