ধরুন আমাদের একটি সংখ্যা n আছে। আমাদের পরীক্ষা করতে হবে n ডাইহেড্রাল প্রাইম কি না। একটি সংখ্যাকে ডাইহেড্রাল প্রাইম বলা হয় যখন সেই সংখ্যাটি নিজেই প্রাইম হয় এবং একই সংখ্যা বা অন্য কোন মৌলিক সংখ্যা 7-সেগমেন্ট ডিসপ্লে ব্যবহার করে ডিসপ্লের ওরিয়েন্টেশন নির্বিশেষে (স্বাভাবিক বা উপরে-নিচে) দেখানো হয়।
সুতরাং, যদি ইনপুট n =1181 এর মত হয়, তাহলে আউটপুট হবে True
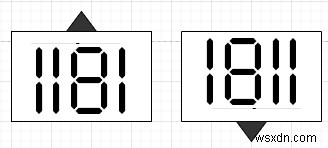
দ্বিতীয়টি প্রথমটির আপ-সাইড ডাউন ফর্ম্যাট এবং দুটিই প্রাইম৷
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- একটি ফাংশন সংজ্ঞায়িত করুন up_side_down()। এটি n লাগবে
- temp :=n, মোট :=0
- যখন temp>
0, do
- d :=টেম্প মোড 10
- যদি d 2 এর সমান হয়, তাহলে d :=5
- অন্যথায় যখন d 5 এর সমান হয়, তখন d :=2
- মোট :=মোট * 10 + d
- temp :=(temp / 10) এর ভাগফল
- মোট রিটার্ন
- প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন:
- যদি n প্রাইম না হয় বা up_side_down(n) প্রাইম না হয় বা n এর রিভার্স প্রাইম না হয় বা up_side_down(n) এর বিপরীত প্রাইম না হয়, তাহলে
- মিথ্যে ফেরত দিন
- তাপ :=n
- যখন temp>
0, do
- rem :=temp mod 10
- যদি rem এই [3, 4, 6, 7, 9] এর যে কোনো একটি হয়, তাহলে
- মিথ্যে ফেরত দিন
- temp :=(temp / 10) এর ভাগফল
- সত্য ফেরান
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
উদাহরণ কোড
prime = (int(1e5)+5)*[True] def reverse(n): return int(str(n)[::-1]) def up_side_down(n): temp = n total = 0 while temp>0: d = temp % 10 if d == 2: d = 5 elif d == 5: d = 2 total = total * 10 + d temp//= 10 return total def get_all_prime(): prime[0] = prime[1] = False for i in range(2, int(1e5)+1): j = 2 while i * j<= int(1e5): prime[i * j] = False j+= 1 def solve(n): get_all_prime() if not prime[n] or not prime[up_side_down(n)] or not prime[reverse(n)] or not prime[reverse(up_side_down(n))]: return False temp = n while temp>0: rem = temp % 10; if rem in [3, 4, 6, 7, 9]: return False temp //= 10 return True n = 1181 print(solve(n))
ইনপুট
23, 3
আউটপুট
True


