পাইথনে একটি বহুভুজকে তার প্রাথমিক অবস্থায় রিসেট করার প্রোগ্রাম

ধরুন, n শীর্ষবিন্দু, n ফ্লিপিং অক্ষ এবং n ঘূর্ণন বিন্দু সহ একটি বহুভুজ রয়েছে। ফ্লিপিং অক্ষ এবং ঘূর্ণন বিন্দুর জন্য নিম্নলিখিতগুলি সত্য

• যদি n বিজোড় হয়, প্রতিটি ফ্লিপিং অক্ষ শুধুমাত্র একটি শীর্ষবিন্দু এবং বিপরীত দিকের মাঝখানের মধ্য দিয়ে যায়।
• যদি n জোড় হয়, অক্ষের অর্ধেকটি বিপরীত শীর্ষবিন্দুর একটি জোড়ার মধ্য দিয়ে যায় এবং বাকি অর্ধেকটি বিপরীত দিকের একটি জোড়ার মধ্য দিয়ে যায়৷
• নিম্নলিখিত দুটি অক্ষের একটি কোণ 360/2n।

এখন, আমরা প্রদত্ত বহুভুজ ঘোরান। আমাদের n বিভিন্ন ধরনের রোটেটর রয়েছে, একটি কে-রোটেটর বহুভুজকে অক্ষ k ঘড়ির কাঁটার দিকে (360 x k)/n ডিগ্রি দ্বারা ঘোরে। একটি তালিকা ইনপুট তালিকা আছে যেটিতে বেশ কয়েকটি জোড়া পূর্ণসংখ্যা রয়েছে। একটি জোড়ার প্রথম পূর্ণসংখ্যা প্রতিনিধিত্ব করে যদি বহুভুজটি ফ্লিপ করা বা ঘোরানো হয়। প্রথম পূর্ণসংখ্যা 1 হলে বহুভুজটি ঘোরানো হয়, যদি এটি 2 হয় বহুভুজটি উল্টানো হয়। দ্বিতীয় পূর্ণসংখ্যাটি হল k, যদি বহুভুজটি ফ্লিপ করা হয় তবে এটি অক্ষ k এ উল্টানো হয় বা অন্যথায়, যদি এটি ঘোরানো হয় তবে এটি 360/2n কোণ দ্বারা ঘোরানো হয়। তালিকাটি খালি না থাকা অবস্থায় ঘূর্ণন এবং ফ্লিপিং করা হয়।

এখানে আমাদের কাজ হল তালিকায় আরেকটি উপাদান যোগ করা যাতে বহুভুজকে তার প্রাথমিক অবস্থানে রিসেট করা যায়।

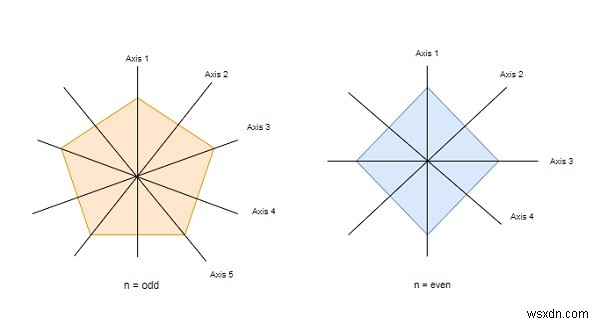
ছবিটি দুই ধরনের বহুভুজের ঘূর্ণন অক্ষগুলিকে নির্দিষ্ট করে৷

সুতরাং, যদি ইনপুটটি n =6, input_list =[[1, 2], [1, 4], [2, 3], [2, 5], [1, 6]] এর মত হয়, তাহলে আউটপুট হবে (1, 4)

রূপান্তরের পরে, 4র্থ অক্ষ বরাবর একটি ঘূর্ণন বহুভুজটিকে তার প্রাথমিক অবস্থানে পুনরায় সেট করবে৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• decision_var :=মিথ্যা
• অবস্থান :=0
• ইনপুট_লিস্টের প্রতিটি আইটেমের জন্য, করুন
  • x :=আইটেম[0]
  • y :=আইটেম[1]
  • যদি x 1 এর মত হয়, তাহলে
    • অবস্থান :=অবস্থান + y
  • অন্যথায়
    • অবস্থান :=y - অবস্থান
    • decision_var :=not(decision_var)
• অবস্থান :=অবস্থান মোড n
• যদি ডিসিশন_ভার অ-শূন্য হয়, তাহলে
  • একটি জোড়া ফেরত দিন (2, অবস্থান)
• অন্যথায়,
  • একটি জোড়া ফেরত দিন (1, n - অবস্থান)

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def solve(n, input_list):
   decision_var = False
   position = 0

   for item in input_list:
      x = item[0]
      y = item[1]
      if x == 1:
         position += y
      else:
         position = y - position
         decision_var = not decision_var
   position = position % n

   if decision_var:
      return (2, position)
   else:
      return (1, n - position)

print(solve(6, [[1, 2], [1, 4], [2, 3], [2, 5], [1, 6]]))

ইনপুট

6, [[1, 2], [1, 4], [2, 3], [2, 5], [1, 6]]

আউটপুট

(1, 4)