পাইথনে একটি পরিষেবা কেন্দ্রের জন্য সর্বোত্তম অবস্থান খোঁজার প্রোগ্রাম

ধরুন আমাদের কাছে অবস্থানের একটি তালিকা রয়েছে, যেখানে স্থানাঙ্ক বিন্দুগুলির একটি তালিকা রয়েছে যেখানে কিছু ঘর অবস্থিত। আপনি যদি (xc, yc) এমন একটি পরিষেবা কেন্দ্র করতে চান যাতে যে কোনও নির্দিষ্ট বিন্দু থেকে (xc, yc) পর্যন্ত ইউক্লিডীয় দূরত্বের যোগফল ন্যূনতম হয়। তাই আমাদের ন্যূনতম দূরত্বের যোগফল বের করতে হবে।

সুতরাং, যদি ইনপুট পজিশনের মত হয় =[(10,11),(11,10),(11,12),(12,11)], তাহলে আউটপুট হবে 4.0

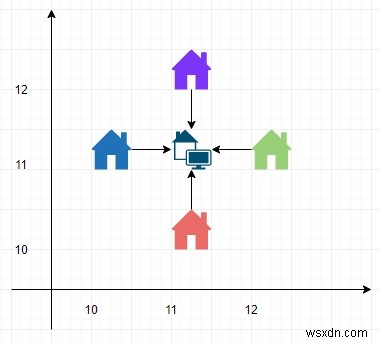
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

numIter :=50
একটি ফাংশন total() সংজ্ঞায়িত করুন। এটি cx, cy, অবস্থান গ্রহণ করবে
মোট :=0.0
পজিশনে প্রতিটি পি এর জন্য, করুন
- x, y :=p
- মোট :=মোট + (cx, cy) এবং (x, y) মধ্যে ইউক্লিডীয় দূরত্ব
মোট রিটার্ন
একটি ফাংশন fy() সংজ্ঞায়িত করুন। এটি x, অবস্থান
নেবে
l :=0, r :=101
res :=0
0 থেকে numIter রেঞ্জের জন্য, করুন
- y1 :=l + (r - l) / 3
- y2 :=r - (r - l) / 3
- t1 :=মোট(x, y1, অবস্থান)
- t2 :=মোট(x, y2, অবস্থান)
- res :=সর্বনিম্ন t1 এবং t2
- যদি t1
  - r :=y2
- অন্যথায়,
  - l :=y1
- রিটার্ন রিটার্ন
- একটি ফাংশন fx() সংজ্ঞায়িত করুন। এটি অবস্থান গ্রহণ করবে
- l :=0, r :=101
- res :=0
- 0 থেকে numIter রেঞ্জের জন্য, করুন
  - x1 :=l + (r - l) / 3
  - x2 :=r - (r - l) / 3
  - t1 :=fy(x1, অবস্থান)
  - t2 :=fy(x2, অবস্থান)
  - res :=সর্বনিম্ন t1 এবং t2
  - যদি t1
    - r :=x2
  - অন্যথায়,
    - l :=x1
- রিটার্ন রিটার্ন

প্রধান পদ্ধতি থেকে, fx(পজিশন)

ফেরত দিন

উদাহরণ

আসুন আরও ভালভাবে বোঝার জন্য নিম্নলিখিত বাস্তবায়ন দেখি

from math import sqrt
def solve(points):
   numIter = 50

   def total(cx, cy, positions):
      total = 0.0
      for p in positions:
         x, y = p
         total += sqrt((cx - x) * (cx - x) + (cy - y) * (cy - y))
      return total

   def fy(x, positions):
      l, r = 0, 101
      res = 0
      for i in range(numIter):
         y1 = l + (r - l) / 3
         y2 = r - (r - l) / 3
         t1 = total(x, y1, positions)
         t2 = total(x, y2, positions)
         res = min(t1, t2)
         if t1 < t2:
            r = y2
         else:
            l = y1
      return res

   def fx(positions):
      l, r = 0, 101
      res = 0
      for i in range(numIter):
         x1 = l + (r - l) / 3
         x2 = r - (r - l) / 3
         t1 = fy(x1, positions)
         t2 = fy(x2, positions)
         res = min(t1, t2)
         if t1 < t2:
            r = x2
         else:
            l = x1
      return res

   return fx(positions)

positions = [(10,11),(11,10),(11,12),(12,11)]
print(solve(positions))

ইনপুট

[(10,11),(11,10),(11,12),(12,11)]

আউটপুট

4.0