একটি গোলকধাঁধায় ইঁদুরও একটি জনপ্রিয় সমস্যা যা ব্যাকট্র্যাকিং ব্যবহার করে। আমি
একটি গোলকধাঁধা হল একটি 2D ম্যাট্রিক্স যাতে কিছু কোষ অবরুদ্ধ থাকে। কোষগুলির মধ্যে একটি হল উৎস কোষ, যেখান থেকে আমাদের শুরু করতে হবে। এবং তাদের মধ্যে আরেকটি হল গন্তব্য, যেখানে আমাদের পৌঁছাতে হবে। আমাদের অবরুদ্ধ কক্ষের কোনোটিতে না গিয়ে উৎস থেকে গন্তব্যে যাওয়ার পথ খুঁজে বের করতে হবে। একটি অমীমাংসিত গোলকধাঁধাটির একটি ছবি নীচে দেখানো হয়েছে৷
৷

এবং এটি তার সমাধান।
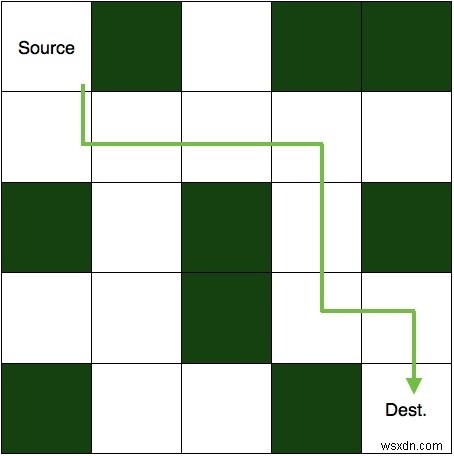
এই ধাঁধাটি সমাধান করার জন্য, আমরা প্রথমে সোর্স সেল দিয়ে শুরু করি এবং এমন একটি দিকে চলে যাই যেখানে পথটি অবরুদ্ধ নয়। পথ যদি আমাদের গন্তব্যে পৌঁছায় তবে ধাঁধার সমাধান হয়ে যায়। অন্যথায়, আমরা ফিরে আসি এবং আমাদের নেওয়া পথের দিক পরিবর্তন করি। আমরা আমাদের কোডেও একই যুক্তি প্রয়োগ করতে যাচ্ছি।
Input:
maze[][] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}}
Output:
1 0 0 0 0
1 1 1 1 0
0 0 0 1 0
0 0 0 1 1
0 0 0 0 1 ব্যাখ্যা
প্রথমত, আমরা গোলকধাঁধাকে উপস্থাপন করার জন্য একটি ম্যাট্রিক্স তৈরি করব এবং ম্যাট্রিক্সের উপাদানগুলি 0 বা 1 হবে। 1 অবরুদ্ধ কোষকে প্রতিনিধিত্ব করবে এবং 0 সেই কোষগুলিকে প্রতিনিধিত্ব করবে যেখানে আমরা সরতে পারি। উপরে দেখানো গোলকধাঁধাটির ম্যাট্রিক্স হল:
0 1 0 1 1 0 0 0 0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 1 0
এখন, আমরা সমাধান সংরক্ষণ করার জন্য একই মাত্রার আরও একটি ম্যাট্রিক্স তৈরি করব। এর উপাদানগুলিও 0 বা 1 হবে৷ 1 আমাদের পথের কোষগুলিকে প্রতিনিধিত্ব করবে এবং বাকি কোষগুলি 0 হবে৷ সমাধানটি প্রতিনিধিত্বকারী ম্যাট্রিক্স হল:
1 0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1
এইভাবে, আমরা এখন আমাদের ম্যাট্রিক্স আছে. এর পরে, আমরা উৎস সেল থেকে গন্তব্য সেলের একটি পথ খুঁজে পাব এবং আমরা যে পদক্ষেপগুলি নেব তা হল:
-
বর্তমান সেলটি পরীক্ষা করুন, যদি এটি গন্তব্য সেল হয়, তাহলে ধাঁধাটি সমাধান করা হয়েছে৷
-
যদি তা না হয়, তাহলে আমরা নিচের দিকে সরে যাওয়ার চেষ্টা করব এবং দেখতে পাব যে আমরা নিচের দিকের কক্ষে যেতে পারি কি না (কোন কক্ষে সরানোর জন্য এটি অবশ্যই খালি হতে হবে এবং আগে থেকেই পথটিতে উপস্থিত নয়)।
-
যদি আমরা সেখানে যেতে পারি, তাহলে আমরা পরবর্তী নিম্নমুখী কক্ষে নিয়ে যাওয়া পথ ধরে চালিয়ে যাব।
-
যদি না হয়, আমরা ডানদিকের ঘরে যাওয়ার চেষ্টা করব। এবং যদি এটি অবরুদ্ধ করা হয় বা নেওয়া হয় তবে আমরা উপরের দিকে চলে যাব।
-
একইভাবে, যদি আমরা উপরে না উঠতে পারি, তাহলে আমরা কেবল বাম ঘরে চলে যাব।
-
যদি চারটি পদক্ষেপের কোনোটিই সম্ভব না হয় (নিচে, ডান, উপরে বা বাম) তবে আমরা কেবল পিছনে সরে যাব এবং আমাদের বর্তমান পথ (ব্যাকট্র্যাকিং) পরিবর্তন করব।
এইভাবে, সংক্ষিপ্তসার হল যে আমরা বর্তমান সেল থেকে অন্য কক্ষে (নিচে, ডান, উপরে এবং বামে) যাওয়ার চেষ্টা করি এবং যদি কোনও নড়াচড়া সম্ভব না হয়, তবে ফিরে এসে অন্য ঘরে যাওয়ার পথের দিক পরিবর্তন করি।
printsolution → এই ফাংশনটি শুধুমাত্র সমাধান ম্যাট্রিক্স প্রিন্ট করছে।
solvemaze → এটি হল আসল ফাংশন যেখানে আমরা ব্যাকট্র্যাকিং অ্যালগরিদম বাস্তবায়ন করছি। প্রথমত, আমরা পরীক্ষা করছি আমাদের সেলটি গন্তব্য সেল কি না যদি (r==SIZE-1) এবং (c==SIZE-1)। যদি এটি গন্তব্য সেল হয় তবে আমাদের ধাঁধা ইতিমধ্যেই সমাধান হয়ে গেছে। যদি না হয়, তাহলে আমরা পরীক্ষা করছি যে এটি একটি বৈধ সেল সরানো বা না। একটি বৈধ ঘর অবশ্যই ম্যাট্রিক্সে থাকতে হবে যেমন, সূচকগুলি অবশ্যই 0 থেকে SIZE-1 r>=0 &&c>=0 &&rউদাহরণ
#include <iostream>
using namespace std;
#define SIZE 5
//the maze problem
int maze[SIZE][SIZE] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}
};
//matrix to store the solution
int solution[SIZE][SIZE];
//function to print the solution matrix
void printsolution() {
int i,j;
for(i=0;i<SIZE;i++) {
for(j=0;j<SIZE;j++) {
printf("%d\t",solution[i][j]);
}
printf("\n\n");
}
}
//function to solve the maze
//using backtracking
int solvemaze(int r, int c) {
//if destination is reached, maze is solved
//destination is the last cell(maze[SIZE-1][SIZE-1])
if((r==SIZE-1) && (c==SIZE-1) {
solution[r][c] = 1;
return 1;
}
//checking if we can visit in this cell or not
//the indices of the cell must be in (0,SIZE-1)
//and solution[r][c] == 0 is making sure that the cell is not already visited
//maze[r][c] == 0 is making sure that the cell is not blocked
if(r>=0 && c>=0 && r<SIZE && c<SIZE && solution[r][c] == 0 && maze[r][c] == 0){
//if safe to visit then visit the cell
solution[r][c] = 1;
//going down
if(solvemaze(r+1, c))
return 1;
//going right
if(solvemaze(r, c+1))
return 1;
//going up
if(solvemaze(r-1, c))
return 1;
//going left
if(solvemaze(r, c-1))
return 1;
//backtracking
solution[r][c] = 0;
return 0;
}
return 0;
}
int main() {
//making all elements of the solution matrix 0
int i,j;
for(i=0; i<SIZE; i++) {
for(j=0; j<SIZE; j++) {
solution[i][j] = 0;
}
}
if (solvemaze(0,0))
printsolution();
else
printf("No solution\n");
return 0;
}


