ব্যাকট্র্যাকিংয়ের ভূমিকা

ব্যাকট্র্যাকিং৷ সমস্যা সমাধানের জন্য অ্যালগরিদমের উপর ভিত্তি করে একটি কৌশল। এটি সময়ের সাথে ধাপে ধাপে মান বৃদ্ধি করে একটি সমাধান তৈরি করে সমাধান খুঁজে পেতে পুনরাবৃত্তিমূলক কলিং ব্যবহার করে। এটি সমাধানগুলিকে সরিয়ে দেয় যা সমস্যার সমাধানের জন্য প্রদত্ত বাধাগুলির উপর ভিত্তি করে সমস্যার সমাধানের জন্ম দেয় না৷

ব্যাকট্র্যাকিং অ্যালগরিদম কিছু নির্দিষ্ট ধরণের সমস্যার জন্য প্রয়োগ করা হয়,

• সমস্যার একটি সম্ভাব্য সমাধান খুঁজে পেতে সিদ্ধান্ত সমস্যা ব্যবহার করা হয়।

• অপ্টিমাইজেশান সমস্যা প্রয়োগ করা যেতে পারে এমন সর্বোত্তম সমাধান খুঁজে পেতে ব্যবহৃত হয়।

• গণনা সমস্যা সমস্যাটির সমস্ত সম্ভাব্য সমাধানের সেট খুঁজে বের করতে ব্যবহৃত হয়।

ব্যাকট্র্যাকিং সমস্যায়, অ্যালগরিদম সমাধানের জন্য একটি সিকোয়েন্স পাথ খুঁজে বের করার চেষ্টা করে যার কিছু ছোট চেকপয়েন্ট আছে যেখান থেকে সমস্যাটি ব্যাকট্র্যাক করতে পারে যদি সমস্যার কোন সম্ভাব্য সমাধান না পাওয়া যায়।

উদাহরণ,

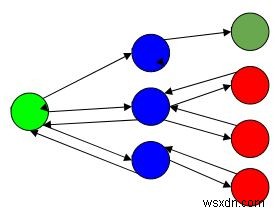
এখানে,

সবুজ হল সূচনা বিন্দু, নীল হল মধ্যবর্তী বিন্দু, লাল হল এমন বিন্দু যার কোন সম্ভাব্য সমাধান নেই, গাঢ় সবুজ হল শেষ সমাধান।

এখানে, যখন অ্যালগরিদমটি একটি সমাধান কিনা তা পরীক্ষা করার জন্য শেষ পর্যন্ত প্রচার করে, যদি এটি হয় তবে সমাধানটি ফেরত দেয় অন্যথায় সমাধান খোঁজার জন্য পরবর্তী পয়েন্টে ট্র্যাক খুঁজতে এটির এক ধাপ পিছনে বিন্দুতে ফিরে যায়।

অ্যালগরিদম

ধাপ 1 − যদি বর্তমান_অবস্থান লক্ষ্য হয়, সফলতা ফেরান ধাপ 2 − অন্যথায়, ধাপ 3 − যদি বর্তমান_পজিশন একটি শেষ বিন্দু হয়, তবে ফেরত ব্যর্থ হয়। ধাপ 4 − অন্যথায়, যদি বর্তমান_পজিশন শেষ বিন্দু না হয়, তাহলে উপরের ধাপগুলি অন্বেষণ করুন এবং পুনরাবৃত্তি করুন। 

 চলুন এই ব্যাকট্র্যাকিং সমস্যাটি ব্যবহার করি N-Queen সমস্যা-এর সমাধান খুঁজতে .
 

 এন-কুইন সমস্যায়, আমাদের একটি এনএক্সএন চেসবোর্ড দেওয়া হয়েছে এবং আমাদের এন রাণীগুলিকে বোর্ডে এমনভাবে রাখতে হবে যাতে কোনও দুই রানী একে অপরকে আক্রমণ না করে। একটি রানী অন্য রানীকে আক্রমণ করবে যদি এটি তার পথে অনুভূমিক, উল্লম্ব বা তির্যক বিন্দুতে স্থাপন করা হয়। এখানে, আমরা 4-কুইন সমস্যা করব।
 

 এখানে, সমাধান হল −
 

 
 

 এখানে, পজিশনে রানী হিসাবে 1 এর সাথে n রানীর সমস্যার জন্য বাইনারি আউটপুট স্থাপন করা হয়েছে।
 
{0 , 1 , 0 , 0}{0 , 0 , 0 , 1}{1 , 0 , 0 , 0}{0 , 0 , 1 , 0}
 

 n কুইন্স সমস্যা সমাধানের জন্য, আমরা রানীকে এক সারির বিভিন্ন অবস্থানে রাখার চেষ্টা করব। এবং এটি অন্য রানীদের সাথে সংঘর্ষ হয় কিনা তা পরীক্ষা করে। রানীদের বর্তমান অবস্থান যদি কোন দুই রানী একে অপরকে আক্রমণ করে থাকে। যদি তারা আক্রমণ করে, আমরা রানীর আগের অবস্থানে ফিরে যাব এবং তার অবস্থান পরিবর্তন করব। এবং আবার রাণীর সংঘর্ষ চেক করুন।
 
অ্যালগরিদম
 
 

 ধাপ 1 - অ্যারেতে 1ম অবস্থান থেকে শুরু করুন।
 ধাপ 2 - বোর্ডে রানী রাখুন এবং পরীক্ষা করুন। করুন, ধাপ 2.1 − রানী রাখার পর, সমাধানের একটি অংশ হিসাবে অবস্থানটি চিহ্নিত করুন এবং তারপরে বারবার পরীক্ষা করুন যে এটি একটি সমাধানের দিকে নিয়ে যাবে কিনা। ধাপ 2.2 − এখন, যদি রানীকে স্থাপন করা কোনো সমাধান এবং ট্র্যাকব্যাকের দিকে না যায় এবং ধাপে যান (a) এবং রানীদের অন্যান্য সারিতে রাখুন। ধাপ 2.3 − যদি রানী স্থাপন করা সমাধানে একটি লিড ফেরত দেয় TRUE. ধাপ 3 − যদি সমস্ত রানীকে রাখা হয় তাহলে সত্য ফেরত দিন। 

 ধাপ 4 − যদি সমস্ত সারি চেষ্টা করা হয় এবং কোন সমাধান না পাওয়া যায়, তাহলে FALSE ফেরত দিন।
 
 

 এখন, Rat in a Maze সমাধান করতে ব্যাকট্র্যাকিং ব্যবহার করুন সমস্যা -
 

 একটি গোলকধাঁধা সমস্যায় ইঁদুরের মধ্যে, আমরা একটি NxN গোলকধাঁধাঁর সাথে ধাঁধাঁর প্রথম অবস্থান অর্থাৎ [0][0] এবং অ্যারের [n-1][n-1] অবস্থানে শেষ করব। এই পথে কিছু মরা রাস্তা আছে যা সমাধানের দিকে নিয়ে যায় না।
 

 এই সমস্যায় ব্যাকট্র্যাকিং ব্যবহার করে আমরা গোলকধাঁধায় চূড়ান্ত লক্ষ্যের অবস্থানে পৌঁছতে ধাপে ধাপে নিচে নামব।
 
নিচের 2D অ্যারে সমস্যাটি কেমন দেখাচ্ছে তা দেখায়৷
৷ 

 
 

 এখানে ড্যাশ করা লাইনগুলি দেখায় যে পথটি ভ্রমণ করা হয়েছে৷
৷