নাম থেকে বোঝা যায়, সমবাহু ত্রিভুজ হল একটি যার সমান বাহু রয়েছে এবং এর প্রতিটির 60° সমান অভ্যন্তরীণ কোণ রয়েছে। এটি নিয়মিত ত্রিভুজ হিসাবেও পরিচিত কারণ এটি একটি নিয়মিত বহুভুজ
সমবাহু ত্রিভুজের বৈশিষ্ট্য হল
- সমান দৈর্ঘ্যের ৩টি বাহু
- একই ডিগ্রির অভ্যন্তরীণ কোণ যা 60
একটি প্লাইগনের বৃত্ত হল সেই বৃত্ত যা একটি বহুভুজের সমস্ত শীর্ষবিন্দুর মধ্য দিয়ে যায়। বৃত্তের ব্যাসার্ধ বৃত্তের অভ্যন্তরে বহুভুজের একটি প্রান্ত বা পার্শ্ব হতে পারে যা বৃত্তাকার নামে পরিচিত এবং বৃত্তের কেন্দ্রটি বৃত্তকেন্দ্র হিসাবে পরিচিত। এটি বৃত্তের ভিতরে বা বাইরে হতে পারে
নীচে একটি সমবাহু ত্রিভুজের বৃত্তের চিত্র দেওয়া হল
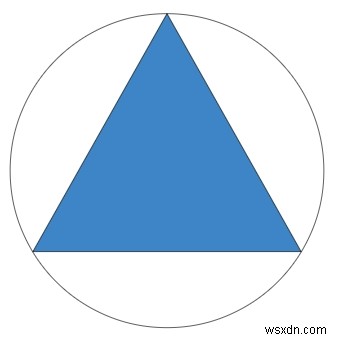
সমস্যা
সমবাহু ত্রিভুজের পাশে দেওয়া কাজটি হল একটি সমবাহু ত্রিভুজের একটি বৃত্তের ক্ষেত্রফল খুঁজে বের করা যেখানে ক্ষেত্রফলটি আকৃতি দ্বারা দখল করা স্থান।
একটি সমবাহু ত্রিভুজের বৃত্তের ক্ষেত্রফল গণনা করার জন্য একটি সূত্র আছে −
Area = (π*a^2)/3
উদাহরণ
Input-: a = 5.0 Output-: Area of CircumCircle of equilateral triangle is :26.1667
অ্যালগরিদম
Start Step 1 -> define macro for pi value #define pi 3.14 Step 2 -> declare function to calculate area of circumcircle of equilateral triangle float area_circum(float a) return (a * a * (pi / 3)) Step 3 -> In main() Declare variables as float a, area Set a = 5 Set area = area_circum(a) Print area Stop
উদাহরণ
#include <iostream>
#include <math.h>
#define pi 3.14
using namespace std;
// function to calculate the area of circumcircle of equilateral triangle
float area_circum(float a){
return (a * a * (pi / 3));
}
int main(){
float a, area;
a = 5.0;
area = area_circum(a);
cout << "Area of CircumCircle of equilateral triangle is :" <<area;
return 0;
} আউটপুট
Area of CircumCircle of equilateral triangle is :26.1667


