ফ্লুরি'স অ্যালগরিদম একটি দिये गये গ্রাফ থেকে ওয়লার পাথ বা ওয়লার সার্কিট প্রদর্শন করতে ব্যবহৃত হয়। এই অ্যালগরিদমে, একটি এজ থেকে শুরু করে, এটি পূর্বের ভের্টেক্স গুলো রিমুভ করে অন্য এডজেসেন্ট ভের্টেক্স গুলোর দিকে যাওয়ার চেষ্টা করে। এই טרিক ব্যবহার করে, গ্রাফটি প্রতিটি ধাপে সিম্পল হয়ে যায় ওয়লার পাথ বা সার্কিট খুঁজে বের করার জন্য।
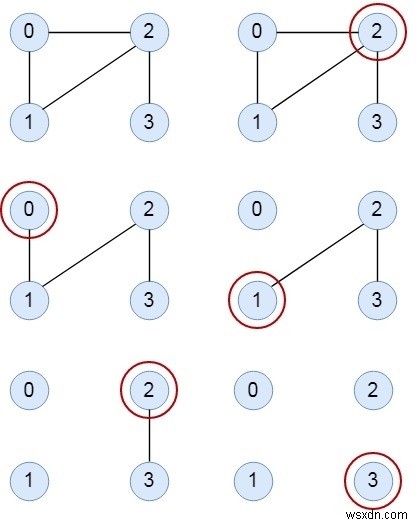
পাথ বা সার্কিট পেতে আমাদের কিছু নিয়ম চেক করতে হবে:
- গ্রাফটি অবশ্যই একটি ওয়লার গ্রাফ হতে হবে।
- যখন দুটি এজ থাকে, একটা ব্রিজ আর একটা নন-ব্রিজ, তবে আমাদের প্রথমে নন-ব্রিজটি বেছে নিতে হবে।
স্টার্টিং ভের্টেক্স নির্বাচনও জটিল। আমরা যেকোনো ভের্টেক্সকে স্টার্টিং ভের্টেক্স হিসেবে ব্যবহার করতে পারি না। যদি গ্রাফের কোনো অড ডিগ্রি ভের্টেক্স না থাকে, তবে আমরা যেকোনো ভের্টেক্সকে স্টার্ট পয়েন্ট হিসেবে বেছে নিতে পারি। অন্যথায়, যখন একটি ভের্টেক্সের অড ডিগ্রি থাকে, তবে আমাদের সেটিকে প্রথমে বেছে নিতে হবে।
ইনপুট
একটি গ্রাফের এডজেসেন্সি ম্যাট্রিক্স
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
আউটপুট
ওয়লার পাথ বা সার্কিট: 1--0 0--2 2--1 1--3 3--0 0--4 4--3 3—2
অ্যালগরিদম
findStartVert(graph)
ইনপুট: দिये गये গ্রাফ। আউটপুট: অ্যালগরিদম শুরু করার জন্য স্টার্টিং ভের্টেক্স খুঁজে বের করা।
শুরু
গ্রাফের সকল ভের্টেক্স i জন্য, করো
deg := 0
i-র সাথে এডজেসেন্ট সকল ভের্টেক্স j জন্য, করো
deg := deg + 1
শেষ
যদি deg অড হয়, তবে
i রিটার্ন করো
শেষ
যখন সকল ডিগ্রি ইভেন হয়, 0 রিটার্ন করো
শেষ
isBridge(u, v)
ইনপুট: স্টার্ট এবং এন্ড নোড। আউটপুট: u এবং v ব্রিজ তৈরি করলে True।
শুরু
deg := 0
v-র সাথে এডজেসেন্ট সকল ভের্টেক্স i জন্য, করো
deg := deg + 1
শেষ
যদি deg > 1, তবে
false রিটার্ন করো
true রিটার্ন করো
শেষ
fleuryAlgorithm(start)
ইনপুট: স্টার্টিং ভের্টেক্স। আউটপুট: ওয়লার পাথ বা সার্কিট প্রদর্শন।
শুরু
edge := গ্রাফে এজ সংখ্যা পাওয়া // এটি পরবর্তী রিকারশন কল-এ ইনিশিয়ালাইজ হবে না
start-র সাথে এডজেসেন্ট সকল ভের্টেক্স v জন্য, করো
যদি edge <= 1 অথবা isBridge(start, v) false হয়, তবে
start এবং v থেকে পাথ ডিসপ্লে করো
গ্রাফ থেকে এজ (start,v) রিমুভ করো
edge ১ কমানো
fleuryAlgorithm(v)
শেষ যদি
শেষ
শেষ
উদাহরণ (C++ কোড)
#include <iostream>
#include <vector>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {{0, 1, 1, 1, 1},
{1, 0, 1, 1, 0},
{1, 1, 0, 1, 0},
{1, 1, 1, 0, 1},
{1, 0, 0, 1, 0} };
int tempGraph[NODE][NODE];
int findStartVert() {
for(int i = 0; i < NODE; i++) {
int deg = 0;
for(int j = 0; j < NODE; j++) {
if(tempGraph[i][j])
deg++; // সংযুক্ত এজ পাওয়া গেলে ডিগ্রি বাড়াও
}
if(deg % 2 != 0) // যখন ভের্টেক্স গুলোর ডিগ্রি অড
return i; // i হল অড ডিগ্রি দিয়ে নোড
}
return 0; // যখন সকল ভের্টেক্সের ডিগ্রি ইভেন, 0 থেকে শুরু করো
}
bool isBridge(int u, int v) {
int deg = 0;
for(int i = 0; i < NODE; i++)
if(tempGraph[v][i])
deg++;
if(deg > 1) {
return false; // এজটি ব্রিজ তৈরি করছে না
}
return true; // এজটি একটি ব্রিজ তৈরি করছে
}
int edgeCount() {
int count = 0;
for(int i = 0; i < NODE; i++)
for(int j = i; j < NODE; j++)
if(tempGraph[i][j])
count++;
return count; // গ্রাফে এজ সংখ্যা কাউন্ট করো
}
void fleuryAlgorithm(int start) {
static int edge = edgeCount();
for(int v = 0; v < NODE; v++) {
if(tempGraph[start][v]) { // যখন (u,v) এজ উপস্থিত এবং ব্রিজ তৈরি করছে না
if(edge <= 1 || !isBridge(start, v)) {
cout << start << "--" << v << " ";
tempGraph[start][v] = tempGraph[v][start] = 0; // গ্রাফ থেকে এজ রিমুভ করো
edge--; // এজ কমানো
fleuryAlgorithm(v);
}
}
}
}
int main() {
for(int i = 0; i < NODE; i++) // মেইন গ্রাফকে tempGraph-এ কপি করো
for(int j = 0; j < NODE; j++)
tempGraph[i][j] = graph[i][j];
cout << "Euler Path Or Circuit: ";
fleuryAlgorithm(findStartVert());
}
আউটপুট
Euler Path Or Circuit: 1--0 0--2 2--1 1--3 3--0 0--4 4--3 3—2
