আমাদের একটি অ্যারে A আছে, আমাদের পরীক্ষা করতে হবে যে অ্যারেটি n লেভেল সহ একটি BST উপস্থাপন করতে পারে কি না। স্তরটি হিসাবে, আমরা নিম্নলিখিত পদ্ধতিতে একটি গাছ তৈরি করতে পারি। অনুমান করুন একটি সংখ্যা k, k-এর চেয়ে বড় মান ডান দিকে চলে যায় এবং k-এর চেয়ে কম বাম দিকে চলে যায়। ধরুন দুটি তালিকা আছে:{50, 20, 9, 25, 10}, এবং {50, 30, 20, 25, 10}
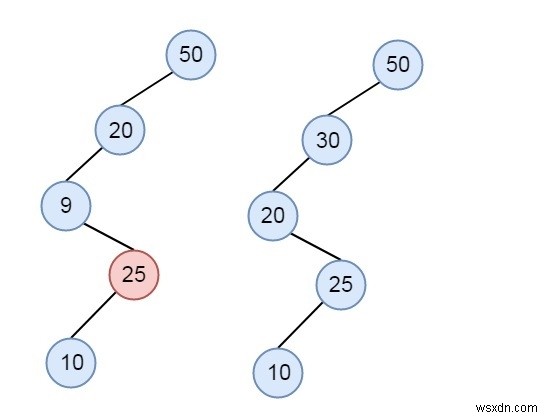
প্রথমটি বৈধ নয়, তবে দ্বিতীয়টি বৈধ৷
৷এটি পরীক্ষা করতে আমরা হয় একটি BST তৈরি করতে পারি এবং উচ্চতা পরীক্ষা করতে পারি, অন্যথায় অ্যারে ভিত্তিক পদ্ধতি ব্যবহার করতে পারি। অ্যারে ভিত্তিক পদ্ধতি নীচের মত -
- বাম সাবট্রির সর্বোচ্চ সীমা চিহ্নিত করতে দুটি পরিবর্তনশীল max =অসীমতা নিন এবং ডান সাবট্রির সর্বনিম্ন সীমা চিহ্নিত করতে min =ঋণাত্মক অসীম নিন
- রেঞ্জ arr[i] থেকে arr[n – 1] এর প্রতিটি উপাদানের জন্য, নিম্নলিখিত ধাপগুলি পুনরাবৃত্তি করুন
- যদি arr[i]> arr[i - 1] এবং arr[i]> min এবং arr[i]
- অন্যথায় যদি arr[i]> min এবং arr[i]
- যদি এগুলোর কোনোটিই বৈধ না হয়, তাহলে উপাদানটিকে একটি নতুন স্তরে ঢোকানো হবে, তাই বিরতি দিন
- অন্যথায় যদি arr[i]> min এবং arr[i]
- যদি arr[i]> arr[i - 1] এবং arr[i]> min এবং arr[i]
উদাহরণ
#include <iostream>
using namespace std;
bool canMakeBSTifHeightN(int arr[], int n) {
int min = INT_MIN;
int max = INT_MAX;
for(int i = 1; i < n; i++){
if (arr[i] > arr[i - 1] && arr[i] > min && arr[i] < max) {
min = arr[i - 1];
} else if (arr[i] < arr[i - 1] && arr[i] > min && arr[i] <
max) {
max = arr[i - 1];
} else {
return true;
}
}
return false;
}
int main() {
int elements[] = {50, 30, 20, 25, 10};
int n = sizeof(elements)/sizeof(elements[0]);
if (canMakeBSTifHeightN(elements, n))
cout << "We can make BST of height " << n;
else
cout << "We can not make BST of height " << n;
} আউটপুট
We can make BST of height 5


