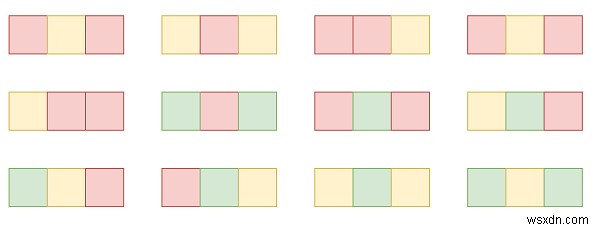
C++ এ N × 3 গ্রিড পেইন্ট করার উপায়ের সংখ্যা

ধরুন আমাদের n x 3 আকারের গ্রিড আছে এবং আমরা গ্রিডের প্রতিটি ঘরকে তিনটি রঙের মধ্যে একটি দিয়ে রং করতে চাই। রং লাল, হলুদ বা সবুজ। এখন একটি সীমাবদ্ধতা রয়েছে যে দুটি সংলগ্ন কোষ একই রঙের নেই। আমাদের গ্রিডের সারির সংখ্যা n আছে। আমরা এই গ্রিড আঁকা উপায় সংখ্যা খুঁজে বের করতে হবে. উত্তরটি খুব বড় হতে পারে তাই এটি মডিউল 10^9 + 7 ফেরত দিন।

সুতরাং, যদি ইনপুট 1 এর মত হয়, তাহলে আউটপুট হবে 12

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

m =1^9 + 7
একটি ফাংশন add() সংজ্ঞায়িত করুন, এটি a, b,
লাগবে
ফিরুন ((a mod m) + (b mod m)) mod m
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
a123 :=6, a121 =6
আরম্ভ করার জন্য i :=2, যখন i <=n, আপডেট করুন (i 1 দ্বারা বাড়ান), করবেন −
- b121 :=যোগ করুন(3 * a121, 2 * a123)
- b123 :=যোগ করুন (2 * a121, 2 * a123)
- a121 :=b121
- a123 :=b123
যোগ করুন(a123, a121)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

#include <bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli mod = 1e9 + 7;
class Solution {
   public:
   lli add(lli a, lli b){
      return ((a % mod) + (b % mod)) % mod;
   }
   int numOfWays(int n){
      lli a123 = 6, a121 = 6;
      lli b123, b121;
      for (int i = 2; i <= n; i++) {
         b121 = add(3 * a121, 2 * a123);
         b123 = add(2 * a121, 2 * a123);
         a121 = b121;
         a123 = b123;
      }
      return add(a123, a121);
   }
};
main(){
   Solution ob;
   cout << (ob.numOfWays(3));
}