ধরুন আমাদের একটি বাইনারি গাছ আছে। আমরা জানি বাইনারি ট্রির সংক্ষিপ্ত এনকোডিং সর্বনিম্ন সম্ভাব্য স্থানের কাছাকাছি কাজ করে। n’ম কাতালান সংখ্যাটি n ভিন্ন নোড সহ কাঠামোগতভাবে ভিন্ন বাইনারি গাছের সংখ্যা দ্বারা মনোনীত হয়। n বড় হলে, এটি প্রায় 4n; সুতরাং, এটিকে এনকোড করার জন্য আমাদের সর্বনিম্ন log2(4) n =2n বিট প্রয়োজন। একটি সংক্ষিপ্ত বাইনারি গাছ তাই 2n + O(n) বিট ব্যবহার করবে।
সুতরাং, যদি ইনপুট মত হয়
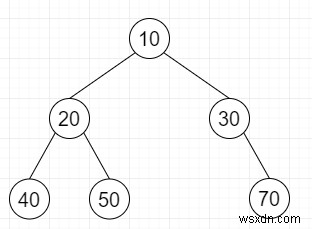
তাহলে আউটপুট হবে
এনকোড করা -
গঠন তালিকা 1 1 1 0 0 1 0 0 1 0 1 0 0
ডেটা তালিকা 10 20 40 50 30 70
ডিকোড করা - উপরে দেখানো গাছ।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- একটি ফাংশন সংজ্ঞায়িত করুন এনকোড(), এটি রুট করবে, স্ট্রাক নামের একটি তালিকা, ডেটা নামের একটি তালিকা,
- যদি রুট NULL এর মত হয়, তাহলে −
- স্ট্রাকের শেষে 0 ঢোকান
- প্রত্যাবর্তন
- স্ট্রাকের শেষে 1 ঢোকান
- ডেটার শেষে রুটের মান সন্নিবেশ করান
- এনকোড (রুট, স্ট্রাক, ডেটার বামে)
- এনকোড (রুট, স্ট্রাক, ডেটার ডানদিকে)
- একটি ফাংশন ডিকোড() সংজ্ঞায়িত করুন, এটি স্ট্রাক নামের একটি তালিকা নেবে, ডেটা নামের একটি তালিকা,
- যদি স্ট্রাকের আকার <=0 হয়, তাহলে −
- NULL ফেরত দিন
- vb :=স্ট্রাকের প্রথম উপাদান
- স্ট্রাক থেকে সামনের উপাদান মুছুন
- যদি b 1 এর সমান হয়, তাহলে −
- কী :=ডেটার প্রথম উপাদান
- ডেটা থেকে সামনের উপাদান মুছুন
- root =কী সহ নতুন নোড
- মূলের বাম :=ডিকোড(স্ট্রাক, ডেটা)
- মূলের ডানদিকে :=ডিকোড(স্ট্রাক, ডেটা)
- রিটার্ন রুট
- NULL ফেরত দিন
উদাহরণ (C++)
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
#include<bits/stdc++.h>
using namespace std;
class TreeNode {
public:
int val;
TreeNode *left, *right;
TreeNode(int data) {
val = data;
left = NULL;
right = NULL;
}
};
void Encode(TreeNode *root, list<bool>&struc, list<int>&data){
if(root == NULL){
struc.push_back(0);
return;
}
struc.push_back(1);
data.push_back(root->val);
Encode(root->left, struc, data);
Encode(root->right, struc, data);
}
TreeNode *Decode(list<bool>&struc, list<int>&data){
if(struc.size() <= 0)
return NULL;
bool b = struc.front();
struc.pop_front();
if(b == 1){
int key = data.front();
data.pop_front();
TreeNode *root = new TreeNode(key);
root->left = Decode(struc, data);
root->right = Decode(struc, data);
return root;
}
return NULL;
}
void preorder_trav(TreeNode* root){
if(root){
cout << "key: "<< root->val;
if(root->left)
cout << " | left child: "<< root->left->val;
if(root->right)
cout << " | right child: "<< root->right->val;
cout << endl;
preorder_trav(root->left);
preorder_trav(root->right);
}
}
main() {
TreeNode *root = new TreeNode(10);
root->left = new TreeNode(20);
root->right = new TreeNode(30);
root->left->left = new TreeNode(40);
root->left->right = new TreeNode(50);
root->right->right = new TreeNode(70);
cout << "The Tree\n";
preorder_trav(root);
list<bool> struc;
list<int> data;
Encode(root, struc, data);
cout << "\nEncoded Tree\n";
cout << "Structure List\n";
list<bool>::iterator si; // Structure iterator
for(si = struc.begin(); si != struc.end(); ++si)
cout << *si << " ";
cout << "\nData List\n";
list<int>::iterator di; // Data iIterator
for(di = data.begin(); di != data.end(); ++di)
cout << *di << " ";
TreeNode *newroot = Decode(struc, data);
cout << "\n\nPreorder traversal of decoded tree\n";
preorder_trav(newroot);
} ইনপুট
root->left = new TreeNode(20); root->right = new TreeNode(30); root->left->left = new TreeNode(40); root->left->right = new TreeNode(50); root->right->right = new TreeNode(70);
আউটপুট
The Tree key: 10 | left child: 20 | right child: 30 key: 20 | left child: 40 | right child: 50 key: 40 key: 50 key: 30 | right child: 70 key: 70 Encoded Tree Structure List 1 1 1 0 0 1 0 0 1 0 1 0 0 Data List 10 20 40 50 30 70 Preorder traversal of decoded tree key: 10 | left child: 20 | right child: 30 key: 20 | left child: 40 | right child: 50 key: 40 key: 50 key: 30 | right child: 70 key: 70


