সি++ এ বাইনারি ট্রিতে সিউডো-প্যালিন্ড্রোমিক পাথ

ধরুন আমাদের একটি বাইনারি ট্রি আছে যেখানে নোডের মানগুলি 1 থেকে 9 পর্যন্ত অঙ্কের। বাইনারি গাছের একটি পথকে ছদ্ম-প্যালিন্ড্রোমিক বলা হয় যখন পথে নোডের মানগুলির অন্তত একটি পরিবর্তন একটি প্যালিনড্রোম হয়। আমাদের রুট নোড থেকে লিফ নোড পর্যন্ত সিউডো-প্যালিন্ড্রোমিক পাথের সংখ্যা খুঁজে বের করতে হবে।

সুতরাং, যদি ইনপুট মত হয়

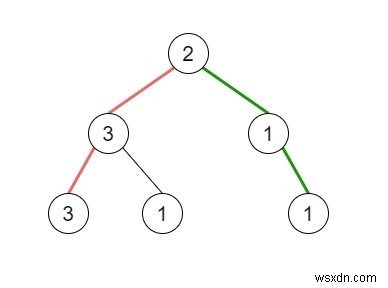
তাহলে আউটপুট হবে 2, এর কারণ হল রুট নোড থেকে লিফ নোডে যাওয়ার তিনটি পথ রয়েছে - লাল পথ অনুসরণ করে [2,3,3], সবুজ পথ অনুসরণ করে [2,1,1], এবং পথ [ 2,3,1]। এই পথগুলির মধ্যে শুধুমাত্র লাল পথ এবং সবুজ পথ হল ছদ্ম-প্যালিন্ড্রোমিক পাথ যেহেতু লাল পথ [2,3,3] কে [3,2,3] হিসাবে পুনর্বিন্যাস করা যেতে পারে এবং সবুজ পথ [2,1,1]কে পুনর্বিন্যাস করা যেতে পারে। যেমন [1,2,1]।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি ফাংশন সংজ্ঞায়িত করুন ok(), এটি একটি অ্যারে v,

  নেবে

• বিজোড় :=0

• প্রতিটি উপাদানের জন্য এটি v −

  • বিজোড় :=বিজোড় + এটি এবং 1

• বিজোড় 0 বা বিজোড় 1 হলে সত্য ফেরত দিন, অন্যথায় মিথ্যা

• একটি ফাংশন সংজ্ঞায়িত করুন dfs(), এটি নোড, অ্যারে v,

  নেবে

• যদি নোড নাল হয়, তাহলে −

  • ফেরত

• 1

  দ্বারা v[নোডের মান] বাড়ান

• যদি নোডের বাম অংশ নাল হয় এবং নোডের ডানদিকে শূন্য হয়, তাহলে −

  • যদি ok(v) সত্য হয়, তাহলে -

    • (রেট 1 দ্বারা বৃদ্ধি করুন)

  • 1

    দ্বারা v[নোডের মান] হ্রাস করুন

  • ফেরত

• dfs(নোডের বাম, v)

• dfs(নোডের ডানদিকে, v)

• 1

  দ্বারা v[নোডের মান] হ্রাস করুন

• প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -

• ret :=0

• 10

  আকারের একটি অ্যারে cnt সংজ্ঞায়িত করুন

• dfs(root, cnt)

• রিটার্ন রিটার্ন

উদাহরণ

আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -

#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
   int val;
   TreeNode *left, *right;
   TreeNode(int data){
      val = data;
      left = NULL;
      right = NULL;
   }
};
void insert(TreeNode **root, int val){
   queue<TreeNode*> q;
   q.push(*root);
   while(q.size()){
      TreeNode *temp = q.front();
      q.pop();
      if(!temp->left){
         if(val != NULL)
            temp->left = new TreeNode(val);
         else
            temp->left = new TreeNode(0);
         return;
      }
      else{
         q.push(temp->left);
      }
      if(!temp->right){
         if(val != NULL)
            temp->right = new TreeNode(val);
         else
            temp->right = new TreeNode(0);
         return;
      }
      else{
         q.push(temp->right);
      }
   }
}
TreeNode *make_tree(vector<int> v){
   TreeNode *root = new TreeNode(v[0]);
   for(int i = 1; i<v.size(); i++){
      insert(&root, v[i]);
   }
   return root;
}
class Solution {
public:
   int ret;
   bool ok(vector <int>& v){
      int odd = 0;
      for (auto& it : v) {
         odd += it & 1;
      }
      return odd == 0 || odd == 1;
   }
   void dfs(TreeNode* node, vector <int>& v){
      if (!node)
         return;
      v[node->val]++;
      if (!node->left && !node->right) {
         if (ok(v))
            ret++;
         v[node->val]--;
         return;
      }
      dfs(node->left, v);
      dfs(node->right, v);
      v[node->val]--;
   }
   int pseudoPalindromicPaths (TreeNode* root) {
      ret = 0;
      vector<int> cnt(10);
      dfs(root, cnt);
      return ret;
   }
};
main(){
   Solution ob;
   vector<int> v = {2,3,1,3,1,NULL,1};
   TreeNode *root = make_tree(v);
   cout << (ob.pseudoPalindromicPaths(root));
}

ইনপুট

{2,3,1,3,1,NULL,1}

আউটপুট

2