দুটি সংখ্যা ই এবং পি দেওয়া হয়েছে৷ লক্ষ্য হল কতগুলি উপায়ে আমরা একটি সেটের e উপাদানগুলিকে p পার্টিশন/সাবসেটে ভাগ করতে পারি।
উদাহরণস্বরূপ
ইনপুট
e=4 p=2
আউটপুট
Count of number of ways to partition a set into k subsets are: 7
ব্যাখ্যা
If elements are: a b c d then ways to divide them into 2 partitions are: (a,b,c)−(d), (a,b)−(c,d), (a,b,c)−(d), (a)−(b,c,d), (a,c)−(b,d), (a,c,d)−(b), (a,b,d)−(c). Total 7 ways.
ইনপুট
e=2 p=2
আউটপুট
Count of number of ways to partition a set into k subsets are: 1
ব্যাখ্যা
If elements are: a b then ways to divide them into 2 partitions are: (a)− (b). Total 1 way only.
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি −
এই পদ্ধতিতে আমরা একটি গতিশীল প্রোগ্রামিং পদ্ধতি ব্যবহার করব। সমাধানে ব্যবহৃত গণনা সবসময় পুনরাবৃত্তিমূলক হবে। যদি আমরা উপাদানগুলিকে p পার্টিশনে ভাগ করি তাহলে -
-
যদি e−1 উপাদানগুলোকে p পার্টিশনে ভাগ করা যায় (e-1,p)। তারপরে আমরা বর্তমান উপাদানগুলিকে এই p পার্টিশনগুলির মধ্যে একটিতে p* উপায়ে (e-1,p) রাখতে পারি।
-
যদি e−1 উপাদানগুলিকে p−1 পার্টিশনে বিভক্ত করা হয় (e−1,p−1) তাহলে সেই পৃথক 1 পার্টিশনে 1টি উপাদান রাখলে 1*ওয়ে (e−1,p−1) থাকবে। মোট উপায় হবে বেপ*ওয়ে(e−1,p)+ওয়েস(e−1,p−1)। এই পদ্ধতিটি পুনরাবৃত্তিমূলক হয়ে উঠবে −
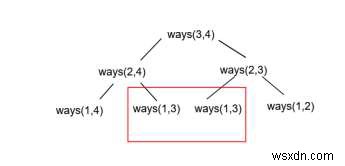
উপরে দেখানো হিসাবে ডুপ্লিকেট গণনা করা হবে. এটি এড়াতে আমরা অ্যাডাইনামিক প্রোগ্রামিং পদ্ধতি ব্যবহার করব।
-
ইনপুট হিসাবে ভেরিয়েবল, উপাদান এবং পার্টিশন নিন।
-
ফাংশন partition_k(int উপাদান, int পার্টিশন) উভয় ভেরিয়েবল নেয় এবং একটি সেটকে k সাবসেটে ভাগ করার উপায়ের সংখ্যা ফেরত দেয়।
-
arr[e][p] এ উপায়(e,p) এর মান সংরক্ষণ করতে 2D অ্যারে অ্যারে[এলিমেন্টস + 1][পার্টিশন + 1] নিন।
-
i=0 থেকে i=elements এ লুপ ব্যবহার করে, arr[i][0] =0 সেট করুন যেহেতু পার্টিশনের সংখ্যা 0 তারপর উপায়(i,0)=0।
-
আবার j=0 থেকে i=partitions-এ লুপ ব্যবহার করে, arr[0][j] =0 সেট করুন কারণ উপাদানের সংখ্যা 0 তারপর উপায়(0,i)=0।
-
এখন ট্রাভার্স arr[][] i=1 থেকে i<=elements এবং j=1 থেকে j<=i পর্যন্ত লুপের জন্য দুটি ব্যবহার করে। এবং বিশ্রামের মান পূরণ করুন।
-
একটি একক উপাদানের জন্য, উপায়=1 বা x উপাদানগুলিকে x পার্টিশনে ভাগ করার জন্য শুধুমাত্র 1টি উপায় রয়েছে। সুতরাং i==j বা j==1 ক্ষেত্রে arr[i][j] =1 সেট করুন।
-
অন্যথায় temp_1 =arr[i−1][j−1] এবং temp_2 =arr[i−1][j] সেট করুন এবং arr[i][j] =j * temp_2 + temp_1 আপডেট করুন।
-
সমস্ত লুপের শেষে আমাদের মোট উপায় হিসাবে arr[elements][partition] থাকবে।
-
ফলাফল হিসাবে arr[elements][partition] ফেরত দিন।
উদাহরণ
#include<iostream>
using namespace std;
int partition_k(int elements, int partition){
int arr[elements + 1][partition + 1];
for(int i = 0; i <= elements; i++){
arr[i][0] = 0;
}
for(int j = 0; j <= partition; j++){
arr[0][partition] = 0;
}
for(int i = 1; i <= elements; i++){
for (int j = 1; j <= i; j++){
if (j == 1 || i == j)
{ arr[i][j] = 1; }
else{
int temp_1 = arr[i−1][j−1];
int temp_2 = arr[i−1][j];
arr[i][j] = j * temp_2 + temp_1;
}
}
}
return arr[elements][partition];
}
int main(){
int elements = 4;
int partition = 2;
cout<<"Count of number of ways to partition a set into k subsets are: "<<partition_k(elements, partition);
return 0;
} আউটপুট
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট −
উৎপন্ন করবেCount of number of ways to partition a set into k subsets are: 7


