সংখ্যা তত্ত্বে সংজ্ঞায়িত একটি গাণিতিক সংখ্যা একটি প্রদত্ত সংখ্যার ভিত্তি হল একটি প্রাকৃতিক সংখ্যা যা অন্য একটি প্রাকৃতিক সংখ্যার নিখুঁত ঘনকের সমান যাতে প্রথম প্রাকৃতিক সংখ্যার অঙ্কের যোগফল দ্বিতীয় সংখ্যার অঙ্কের যোগফলের সমান হয়। em> (উইকিপিডিয়া)।
নম্বরটি হেনরি ডুডেনি খুঁজে পেয়েছেন . এর গাণিতিক সূত্র হল −
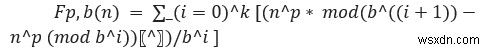
এখানে, আমরা একটি পূর্ণসংখ্যা n দেওয়া হয়. আমাদের কাজ হল প্রদত্ত সংখ্যা n একটি ডুডেনি নম্বর কিনা তা পরীক্ষা করা।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট: N =17592
আউটপুট: না
ব্যাখ্যা:
প্রদত্ত নম্বরটি একটি ডুডনি নম্বর নয়৷
৷সমাধান পদ্ধতি -
সমাধানটি dudeney সংখ্যার মৌলিক সংজ্ঞায় রয়েছে। একটি সংখ্যা হল একটি ডুডেনি সংখ্যা এই তথ্যের ভিত্তিতে যে একটি সংখ্যার ঘনমূল তার অঙ্কের যোগফলের সমান .
অ্যালগরিদম −
ধাপ 1: n একটি নিখুঁত ঘনক কিনা তা পরীক্ষা করুন।
ধাপ 2.1: যদি হ্যাঁ, তাহলে n এর ঘনমূল =n এর অঙ্কের যোগফল কিনা তা পরীক্ষা করে দেখুন।
ধাপ 2.2.1: যদি হ্যাঁ, তাহলে নম্বরটি হল ডুডেনি নম্বর।
ধাপ 2.2.2: যদি NO হয়, তাহলে সংখ্যাটি Dudeney নম্বর নয়।
ধাপ 2.2: যদি না হয়, তাহলে নম্বরটি ডুডেনি নম্বর নয়৷
৷আমাদের অ্যালগরিদমের কাজ চিত্রিত করার জন্য C++ প্রোগ্রাম -
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
int calcDigitSum(int n){
int digitSum = 0;
int digitVal;
while (n > 0) {
digitVal = n % 10;
digitSum += digitVal;
n /= 10;
}
return digitSum;
}
int checkDudeney(int N) {
int cubeRoot = int( round( cbrt(N) ) );
if(pow(cubeRoot, 3.0) != N){
return 0;
}
int sumOfDigit = calcDigitSum(N);
if (cubeRoot != sumOfDigit)
return 0;
return 1;
}
int main() {
int N = 104323;
cout<<"The number "<<N;
if (checkDudeney(N))
cout<<" is a dudeney number.";
else
cout<<" is not a dudeney number.";
return 0;
} আউটপুট −
The number 104323 is not a dudeney number.৷


