এই সমস্যায়, আমরা একটি বাইনারি গাছ দেওয়া হয়. আমাদের কাজ হল একটি বাইনারি গাছের ন্যূনতম গভীরতা খুঁজে বের করা।
বাইনারি ট্রির একটি বিশেষ শর্ত রয়েছে যে প্রতিটি নোডে সর্বাধিক দুটি সন্তান থাকতে পারে৷
একটি বাইনারি গাছের ন্যূনতম গভীরতা হল রুট নোড থেকে যেকোনো লিফ নোডের মধ্যে সবচেয়ে ছোট পথ।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
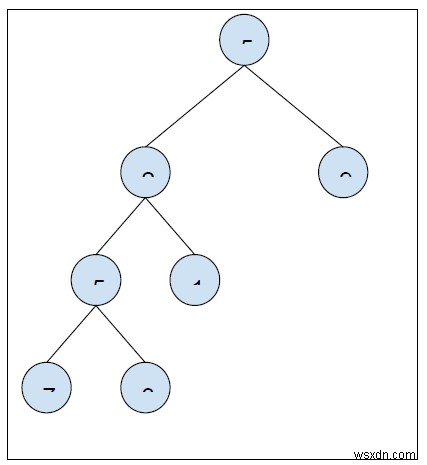
আউটপুট
2
সমাধান পদ্ধতি
সমস্যার সমাধান হল বাইনারি ট্রি অতিক্রম করা এবং উচ্চতা গণনা করা। প্রতিটি নোড নন-লিফ নোডের জন্য নোডের চাইল্ড নোডের জন্য বারবার কল করে এবং প্রতিটি লিফ নোডের জন্য 1 ফেরত দিয়ে এটি করা যেতে পারে।
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
উদাহরণ
#include<bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node* left, *right;
};
int findMinDepthBT(Node *currentNode) {
if (currentNode == NULL)
return 0;
if (currentNode->left == NULL && currentNode->right == NULL)
return 1;
if (!currentNode->left)
return findMinDepthBT(currentNode->right) + 1;
if (!currentNode->right)
return findMinDepthBT(currentNode->left) + 1;
return min(findMinDepthBT(currentNode->left),
findMinDepthBT(currentNode->right)) + 1;
}
Node *newNode(int data) {
Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return (temp);
}
int main() {
Node *root = newNode(5);
root->left = newNode(2);
root->right = newNode(9);
root->left->left = newNode(5);
root->left->right = newNode(1);
root->left->left->left = newNode(7);
root->left->left->right = newNode(3);
cout<<"The minimum depth of binary tree is "<<findMinDepthBT(root);
return 0;
} আউটপুট
The minimum depth of binary tree is 2
এই পদ্ধতিটি বেশ দক্ষ কিন্তু আমরা আরও কার্যকরভাবে ন্যূনতম গভীরতা খুঁজে পেতে অন্যান্য ট্রাভার্সাল কৌশলগুলি ব্যবহার করতে পারি৷
এই ধরনের একটি পদ্ধতি হল লেভেল অর্ডার ট্রাভার্সাল ব্যবহার করা যেখানে আমরা গাছের স্তরকে স্তর দ্বারা অতিক্রম করি। এবং আমরা যে লেভেল নম্বরে আমাদের প্রথম লিফ নোডের সম্মুখীন হব তা ফেরত দেব।
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম,
উদাহরণ
#include<bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
struct lOrderQueue {
Node *node;
int depth;
};
int findMinDepthBT(Node *root) {
if (root == NULL)
return 0;
queue<lOrderQueue> levelOrder;
lOrderQueue deQueue = {root, 1};
levelOrder.push(deQueue);
while (levelOrder.empty() == false) {
deQueue = levelOrder.front();
levelOrder.pop();
Node *node = deQueue.node;
int depth = deQueue.depth;
if (node->left == NULL && node->right == NULL)
return depth;
if (node->left != NULL) {
deQueue.node = node->left;
deQueue.depth = depth + 1;
levelOrder.push(deQueue);
}
if (node->right != NULL) {
deQueue.node = node->right;
deQueue.depth = depth+1;
levelOrder.push(deQueue);
}
}
return 0;
}
Node* newNode(int data) {
Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
int main() {
Node *root = newNode(5);
root->left = newNode(2);
root->right = newNode(9);
root->left->left = newNode(5);
root->left->right = newNode(1);
root->left->left->left = newNode(7);
root->left->left->right = newNode(3);
cout<<"The minimum depth of binary tree is "<<findMinDepthBT(root);
return 0;
} আউটপুট
The minimum depth of binary tree is 2


