এই সমস্যায়, আমাদেরকে একটি রেখার শুরু বিন্দু A(xA) এর দুটি বিন্দুর স্থানাঙ্ক দেওয়া হয়েছে , yA ) এবং মধ্যবিন্দু M(xM , yM ) .আমাদের কাজ হল প্রদত্ত এক প্রান্ত এবং মাঝামাঝি সহ একটি রেখার অন্য প্রান্ত বিন্দু খুঁজে বের করা .
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট
A = [1, 2], M = [3, 0]
আউটপুট
[5, -2]
ব্যাখ্যা
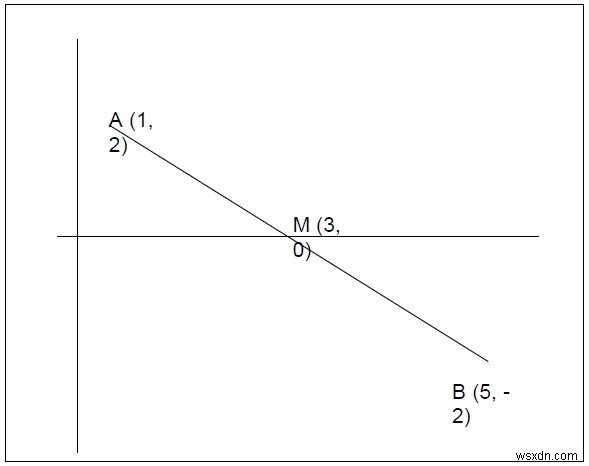
লাইনটি হল −
সমাধান পদ্ধতি
সমস্যা সমাধানের জন্য, আমরা গণিতে শিখেছি জ্যামিতির ধারণাগুলি ব্যবহার করব। আপনি যদি মনে করেন প্রতিটি লাইনের জন্য একটি মধ্যবিন্দু সূত্র রয়েছে যা হল,
mid(x) = (x1 + x2) / 2 mid(y) = (y1 + y2) / 2
কিন্তু আমাদের সমস্যার মধ্যবিন্দুর মান দেওয়া হয়েছে এবং x2 এবং y2-এর মান প্রয়োজন। সুতরাং, আমরা সেই অনুযায়ী সূত্র পরিবর্তন করব।
x2 = 2*mid(x) - x1 y2 = 2*mid(y) - y1
উপরের সূত্রটি ব্যবহার করে, আমরা মধ্যবিন্দু এবং লাইনের একটি বিন্দু ব্যবহার করে অন্য শেষ বিন্দুর মান খুঁজে পেতে পারি।
উদাহরণ
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম
#include <iostream>
using namespace std;
void findMissingPointLine(float x1, float y1, float xm, float ym){
float x2 = (2 * xm) - x1;
float y2 = (2 * ym) - y1;
cout<<"B(x, y) = "<<"( "<<x2<<", "<<y2<<" )";
}
int main()
{
float x1 = -4, y1 = -1, xm = 3, ym = 5;
cout<<"The other end point of the line is \n";
findMissingPointLine(x1, y1, xm, ym);
return 0;
} আউটপুট
The other end point of the line is B(x, y) = ( 10, 11 )


