নির্দিষ্ট শর্তের সাথে গ্রাফ তৈরি করার জন্য C++ প্রোগ্রাম

ধরুন আমাদের দুটি সংখ্যা N এবং K আছে। বিবেচনা করুন N উপাদান সহ একটি অনির্দেশিত গ্রাফ রয়েছে। N শীর্ষবিন্দুগুলি নিম্নলিখিত শর্তগুলিকে সন্তুষ্ট করে -

গ্রাফটি সহজ এবং সংযুক্ত
শীর্ষবিন্দুগুলি 1 থেকে N
পর্যন্ত সংখ্যাযুক্ত
গ্রাফের প্রান্তের সংখ্যা M হল। প্রান্তগুলি 1 থেকে M পর্যন্ত সংখ্যাযুক্ত। প্রান্তের দৈর্ঘ্য 1। এবং প্রান্ত i শীর্ষবিন্দু U[i]-কে V[i]-এর সাথে সংযুক্ত করে।
ঠিক K জোড়া শীর্ষবিন্দু রয়েছে (i, j) যেখানে i

এই ধরনের গ্রাফ বিদ্যমান থাকলে, আমাদের সেই গ্রাফটি তৈরি করতে হবে। অন্যথায় ফিরুন -1।

সুতরাং, যদি ইনপুটটি N =5 এর মত হয়; K =3, তাহলে আউটপুট হবে

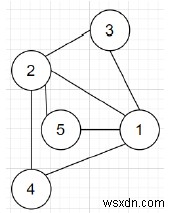
পদক্ষেপ

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

if k > (n - 1) * (n - 2) / 2, then:
   print -1
print ((n - 1) * (n - 2) / 2 - k + n - 1)
for initialize i := 1, when i < n, update (increase i by 1), do:
   print pair (1, i + 1)
count := (n - 1) * (n - 2) / 2 - k
for initialize i := 2, when i <= n, update (increase i by 1), do:
   for initialize j := i + 1, when j <= n, update (increase j by 1), do:
      if count <= 0, then:
         return
      print pair (i, j)
      (decrease count by 1)

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

#include <bits/stdc++.h>
using namespace std;

void solve(int n, int k){
   if (k > (n - 1) * (n - 2) / 2){
      cout << -1 << endl;
   }
   cout << (n - 1) * (n - 2) / 2 - k + n - 1 << '\n';
   for (int i = 1; i < n; i++){
      cout << 1 << ", " << i + 1 << '\n';
   }
   int count = (n - 1) * (n - 2) / 2 - k;
   for (int i = 2; i <= n; i++){
      for (int j = i + 1; j <= n; j++){
         if (count <= 0){
            return;
         }
         cout << i << ", " << j << '\n';
         count--;
      }
   }
}
int main(){
   int N = 5;
   int K = 3;
   solve(N, K);
}

ইনপুট

5, 3

আউটপুট