প্রিমের অ্যালগরিদম হল একটি লোভী অ্যালগরিদম যা একটি ওজনযুক্ত অনির্দেশিত গ্রাফের জন্য একটি ন্যূনতম স্প্যানিং ট্রি খুঁজে পায়৷ এটি প্রান্তগুলির একটি উপসেট খুঁজে পায় যা একটি গাছ গঠন করে যাতে প্রতিটি শীর্ষবিন্দু অন্তর্ভুক্ত থাকে, যেখানে গাছের সমস্ত প্রান্তের মোট ওজন ন্যূনতম হয়৷
অ্যালগরিদম এই ট্রিটিকে একবারে একটি শীর্ষবিন্দু তৈরি করে, একটি নির্বিচারে শুরুর শীর্ষ থেকে, প্রতিটি ধাপে গাছ থেকে অন্য শীর্ষে সবচেয়ে সস্তা সম্ভাব্য সংযোগ যোগ করে কাজ করে৷
প্রিমের অ্যালগরিদম কীভাবে কাজ করে?
প্রিমের অ্যালগরিদম কীভাবে কাজ করে তার একটি চিত্র দেখা যাক −
1. রুট নোড হিসাবে যেকোন আরবিট্রারি নোড বেছে নিন:এই ক্ষেত্রে, আমরা প্রাইমের স্প্যানিং ট্রির রুট নোড হিসাবে S নোড বেছে নিই। এই নোডটি নির্বিচারে বেছে নেওয়া হয়েছে, তাই যেকোনো নোড রুট নোড হতে পারে। কেউ ভাবতে পারে কেন যেকোন ভিডিও রুট নোড হতে পারে। সুতরাং উত্তর হল, স্প্যানিং ট্রিতে একটি গ্রাফের সমস্ত নোড অন্তর্ভুক্ত করা হয়েছে এবং এটি সংযুক্ত থাকায় কমপক্ষে একটি প্রান্ত থাকতে হবে, যা এটিকে বাকি গাছের সাথে যুক্ত করবে।
2. বহির্গামী প্রান্তগুলি পরীক্ষা করুন এবং কম খরচে একটি নির্বাচন করুন:রুট নোড S নির্বাচন করার পরে, আমরা দেখতে পাই যে S, A, এবং S, C দুটি প্রান্তের ওজন যথাক্রমে 7 এবং 8। আমরা প্রান্ত S, A বেছে নিই কারণ এটি অন্যটির চেয়ে কম।
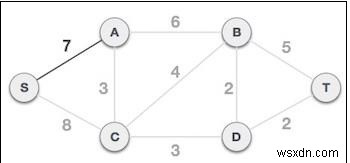
এখন, S-7-A গাছটিকে একটি নোড হিসাবে বিবেচনা করা হয় এবং আমরা এটি থেকে বেরিয়ে আসা সমস্ত প্রান্তগুলি পরীক্ষা করি। আমরা সবচেয়ে কম খরচের একটি নির্বাচন করি এবং এটি গাছের মধ্যে অন্তর্ভুক্ত করি।
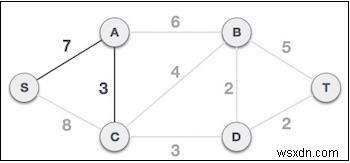
এই ধাপের পরে, S-7-A-3-C গাছ গঠিত হয়। এখন আমরা আবার এটিকে একটি নোড হিসাবে বিবেচনা করব এবং সমস্ত প্রান্ত আবার পরীক্ষা করব। যাইহোক, আমরা শুধুমাত্র সর্বনিম্ন খরচ প্রান্ত নির্বাচন করব. এই ক্ষেত্রে, C-3-D হল নতুন প্রান্ত, যা অন্যান্য প্রান্তের খরচ 8, 6, 4, ইত্যাদির চেয়ে কম৷
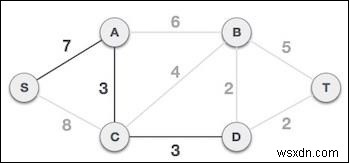
নোড D যোগ করার পর বিস্তৃত গাছের দিকে, আমাদের এখন এর থেকে দুটি প্রান্ত বেরিয়ে যাচ্ছে যার দাম একই, যেমন D-2-T এবং D-2-B। এইভাবে, আমরা যেকোনো একটি যোগ করতে পারি। কিন্তু পরবর্তী ধাপে আবার সর্বনিম্ন খরচ হিসাবে প্রান্ত 2 পাওয়া যাবে। তাই, আমরা একটি বিস্তৃত গাছ দেখাচ্ছি যার উভয় প্রান্ত রয়েছে।
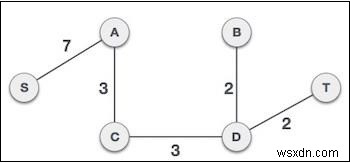
এখন দেখা যাক কিভাবে আমরা আমাদের কোড −
-এ এটি প্রয়োগ করতে পারিউদাহরণ
primsMST() {
// Initialize graph that'll contain the MST
const MST = new Graph();
if (this.nodes.length === 0) {
return MST;
}
// Select first node as starting node
let s = this.nodes[0];
// Create a Priority Queue and explored set
let edgeQueue = new PriorityQueue(this.nodes.length * this.nodes.length);
let explored = new Set();
explored.add(s);
MST.addNode(s);
// Add all edges from this starting node to the PQ taking weights as priority
this.edges[s].forEach(edge => {
edgeQueue.enqueue([s, edge.node], edge.weight);
});
// Take the smallest edge and add that to the new graph
let currentMinEdge = edgeQueue.dequeue();
while (!edgeQueue.isEmpty()) {
// COntinue removing edges till we get an edge with an unexplored node
while (!edgeQueue.isEmpty() && explored.has(currentMinEdge.data[1])) {
currentMinEdge = edgeQueue.dequeue();
}
let nextNode = currentMinEdge.data[1];
// Check again as queue might get empty without giving back unexplored element
if (!explored.has(nextNode)) {
MST.addNode(nextNode);
MST.addEdge(currentMinEdge.data[0], nextNode, currentMinEdge.priority);
// Again add all edges to the PQ
this.edges[nextNode].forEach(edge => {
edgeQueue.enqueue([nextNode, edge.node], edge.weight);
});
// Mark this node as explored explored.add(nextNode);
s = nextNode;
}
}
return MST;
} আপনি এটি ব্যবহার করে পরীক্ষা করতে পারেন:
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C", 100);
g.addEdge("A", "B", 3);
g.addEdge("A", "D", 4);
g.addEdge("C", "D", 3);
g.addEdge("D", "E", 8);
g.addEdge("E", "F", 10);
g.addEdge("B", "G", 9);
g.primsMST().display(); আউটপুট
এটি আউটপুট দেবে −
A->B, D B->A, G D->A, C, E C->D E->D, F G->B F->E
মনে রাখবেন যে আমাদের প্রাথমিক গ্রাফ ছিল −
উদাহরণ
/** * A * / | \ * C | B * \ | | * D G * | / * E * | * F */
আউটপুট
আমাদের বর্তমান গ্রাফ −
এর মত দেখাচ্ছে/** * A * |\ * C | B * \ | | * D G * | * E * | * F * */
আমরা সবচেয়ে ব্যয়বহুল প্রান্তগুলি সরিয়ে ফেলেছি এবং এখন একটি বিস্তৃত গাছ রয়েছে৷


