জাভাস্ক্রিপ্ট ট্রিতে পোস্ট-অর্ডার ট্রাভার্সাল

এই ট্রাভার্সাল পদ্ধতিতে, রুট নোডটি শেষ দেখা হয়, তাই নাম। প্রথমে আমরা বাম সাবট্রি, তারপর ডান সাবট্রি এবং শেষে রুট নোড অতিক্রম করি।

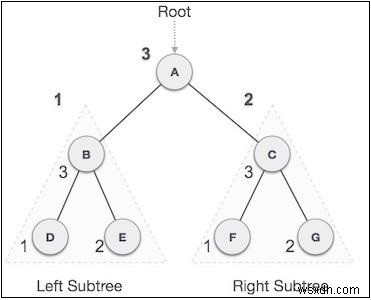
আমরা A, থেকে শুরু করি এবং পোস্ট-অর্ডার ট্রাভার্সাল অনুসরণ করে, আমরা প্রথমে বাম সাবট্রি পরিদর্শন করিB. বি এছাড়াও পোস্ট অর্ডার অতিক্রম করা হয়. সমস্ত নোড পরিদর্শন না হওয়া পর্যন্ত প্রক্রিয়াটি চলতে থাকে। এই গাছের পোস্ট-অর্ডার ট্রাভার্সালের আউটপুট হবে −

D → E → B → F → G → C → A

এটি হল অ্যালগরিদম যা আমরা বাস্তবায়ন করব −

পুনরাবৃত্তভাবে বাম সাবট্রি অতিক্রম করুন
পুনরাবৃত্তভাবে ডান সাবট্রি অতিক্রম করুন
নোডের ডেটা প্রিন্ট করুন

আসুন দেখি কিভাবে আমরা আমাদের ক্লাসে এটি বাস্তবায়ন করব।

postOrder() {
   postOrderHelper(this.root);
}

হেল্পার ফাংশন -

উদাহরণ

function postOrderHelper(root) {
   if (root !== null) {
      postOrderHelper(root.left);
      postOrderHelper(root.right);
      console.log(root.data);
   }
}

আপনি −

ব্যবহার করে এটি পরীক্ষা করতে পারেন

উদাহরণ

let BST = new BinarySearchTree();
BST.insertRec(10);
BST.insertRec(15);
BST.insertRec(5);
BST.insertRec(50);
BST.insertRec(3);
BST.insertRec(7);
BST.insertRec(12);
BST.postOrder();

আউটপুট

এটি আউটপুট দেবে −