DFS ভাইবোন শীর্ষবিন্দু পরিদর্শন করার আগে শিশু শীর্ষবিন্দু পরিদর্শন করে; অর্থাৎ, এটি তার প্রস্থ অন্বেষণ করার আগে কোনো নির্দিষ্ট পথের গভীরতা অতিক্রম করে। অ্যালগরিদম প্রয়োগ করার সময় একটি স্ট্যাক (প্রায়শই প্রোগ্রামের কল স্ট্যাক) সাধারণত ব্যবহৃত হয়।
একটি DFS কিভাবে কাজ করে তা নিচে দেওয়া হল −
- সংলগ্ন অপ্রদর্শিত শীর্ষবিন্দুতে যান। এটি পরিদর্শন হিসাবে চিহ্নিত করুন। এটি প্রদর্শন করুন। এটিকে একটি স্ট্যাকের মধ্যে পুশ করুন৷
- কোন সন্নিহিত শীর্ষবিন্দু পাওয়া না গেলে, স্ট্যাক থেকে একটি শীর্ষবিন্দু পপ আপ করুন। (এটি স্ট্যাক থেকে সমস্ত শীর্ষবিন্দুগুলিকে পপ আপ করবে, যার সংলগ্ন শীর্ষবিন্দু নেই৷)
- স্ট্যাকটি খালি না হওয়া পর্যন্ত নিয়ম 1 এবং নিয়ম 2 পুনরাবৃত্তি করুন৷
আসুন কিভাবে DFS ট্রাভার্সাল কাজ করে তার একটি দৃষ্টান্ত দেখি।
| ধাপ | ট্রাভার্সাল | বিবরণ |
|---|---|---|
| 1 |  | স্ট্যাক শুরু করুন। |
| 2 | 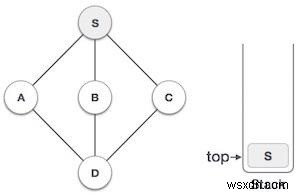 | S চিহ্নিত করুন পরিদর্শন এবং স্ট্যাকের উপর রাখা. S থেকে যেকোন অনাদর্শিত সংলগ্ন নোড অন্বেষণ করুন . আমাদের তিনটি নোড আছে এবং আমরা তাদের যেকোনো একটি বাছাই করতে পারি। এই উদাহরণের জন্য, আমরা নোডটিকে একটি বর্ণানুক্রমিক ক্রমে নেব। |
| 3 | 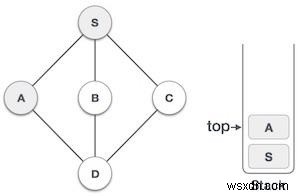 | মার্ক A পরিদর্শন এবং স্ট্যাকের উপর রাখা. A থেকে যেকোন অনাদর্শিত সংলগ্ন নোড অন্বেষণ করুন . উভয়ই S এবং D A এর সংলগ্ন কিন্তু আমরা শুধুমাত্র অনাবিষ্কৃত নোডের জন্য উদ্বিগ্ন। |
| 4 | 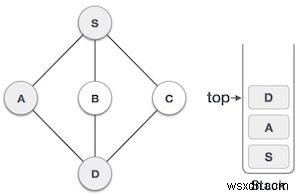 | D দেখুন এবং এটি পরিদর্শন হিসাবে চিহ্নিত করুন এবং স্ট্যাকের উপর রাখুন। এখানে, আমাদের আছে B এবং C নোড, যা D এর সংলগ্ন এবং উভয়ই অদর্শিত। যাইহোক, আমরা আবার একটি বর্ণানুক্রমিক ক্রমে নির্বাচন করব। |
| 5 | 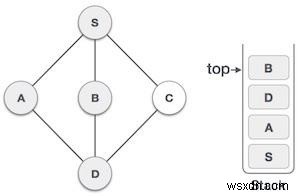 | আমরা B, বেছে নিই এটি পরিদর্শন হিসাবে চিহ্নিত করুন এবং স্ট্যাকের উপর রাখুন। এখানে B কোন অদর্শিত সংলগ্ন নোড নেই. সুতরাং, আমরা B পপ করি স্ট্যাক থেকে |
| 6 | 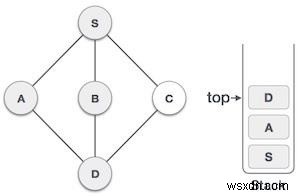 | আগের নোডে ফিরে আসার জন্য আমরা স্ট্যাক টপটি পরীক্ষা করি এবং এটিতে কোনো অনাভিদর্শিত নোড আছে কিনা তা পরীক্ষা করি। এখানে, আমরা D পাই স্ট্যাকের শীর্ষে থাকা। |
| 7 | 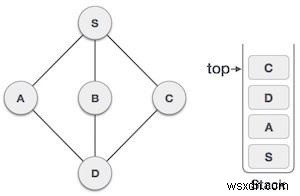 | শুধুমাত্র দেখা না করা সংলগ্ন নোড D থেকে হল C এখন তাই আমরা C, পরিদর্শন করি এটি পরিদর্শন হিসাবে চিহ্নিত করুন এবং স্ট্যাকের উপর রাখুন। |
C হিসাবে কোন অনাদর্শিত সংলগ্ন নোড নেই তাই আমরা স্ট্যাকটি পপ করতে থাকি যতক্ষণ না আমরা একটি নোড খুঁজে পাই যার একটি অদর্শিত সংলগ্ন নোড রয়েছে। এই ক্ষেত্রে, কোনটি নেই এবং স্ট্যাকটি খালি না হওয়া পর্যন্ত আমরা পপিং করতে থাকি। আসুন দেখি কিভাবে আমরা জাভাস্ক্রিপ্টে এটি বাস্তবায়ন করতে পারি।
উদাহরণ
DFS(node) {
// Create a Stack and add our initial node in it
let s = new Stack(this.nodes.length);
let explored = new Set();
s.push(node);
// Mark the first node as explored
explored.add(node);
// We'll continue till our Stack gets empty
while (!s.isEmpty()) {
let t = s.pop();
// Log every element that comes out of the Stack
console.log(t);
// 1. In the edges object, we search for nodes this node is directly connected to.
// 2. We filter out the nodes that have already been explored.
// 3. Then we mark each unexplored node as explored and push it to the Stack.
this.edges[t]
.filter(n => !explored.has(n))
.forEach(n => {
explored.add(n);
s.push(n);
});
}
} ওয়েল, যে সহজ ছিল. আমরা সত্যিই স্ট্যাক এবং voila জন্য সারি আউট অদলবদল, আমরা DFS আছে. এটি সত্যিই 2 এর মধ্যে একমাত্র পার্থক্য। ডিএফএসও পুনরাবৃত্তি ব্যবহার করে প্রয়োগ করা যেতে পারে। তবে এই ক্ষেত্রে এটি এড়ানো ভাল কারণ একটি বড় গ্রাফ মানে কল স্ট্যাকের ট্র্যাক রাখার জন্য আমাদের অতিরিক্ত মেমরির প্রয়োজন৷
আপনি −
ব্যবহার করে এটি পরীক্ষা করতে পারেনlet g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C");
g.addEdge("A", "B");
g.addEdge("A", "D");
g.addEdge("D", "E");
g.addEdge("E", "F");
g.addEdge("B", "G");
g.DFS("A"); আউটপুট
এটি আউটপুট দেবে।
A D E F B G C


