একটি সংক্ষিপ্ততম পথ দেওয়ার পরিবর্তে, ইয়েনের k-ছোটতম পাথ অ্যালগরিদম দেয় k সংক্ষিপ্ততম পথ যাতে আমরা দ্বিতীয় সংক্ষিপ্ততম পথ এবং তৃতীয় সংক্ষিপ্ততম পথটি পেতে পারি।
আসুন আমরা একটি দৃশ্য বিবেচনা করি যে আমাদের স্থান A থেকে B স্থানে ভ্রমণ করতে হবে এবং স্থান A এবং B স্থানের মধ্যে একাধিক রুট উপলব্ধ আছে, কিন্তু আমাদেরকে সবচেয়ে সংক্ষিপ্ততম পথটি খুঁজে বের করতে হবে এবং এর পরিপ্রেক্ষিতে কম বিবেচনা করা হয় এমন সমস্ত পথকে অবহেলা করতে হবে। গন্তব্যে পৌঁছানোর জন্য সময় জটিলতা।
একটি উদাহরণ দিয়ে বোঝা যাক-
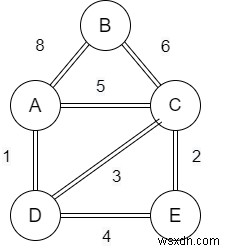
প্রদত্ত উদাহরণটিকে B-এর চূড়াযুক্ত সেতু হিসাবে বিবেচনা করুন। যদি কেউ A থেকে C পর্যন্ত সেতুটি অতিক্রম করতে চায়, তবে কেউ সেতুটি অতিক্রম করতে শিখরে যাবে না। সুতরাং এটি A থেকে C পর্যন্ত কিছুটা দীর্ঘ পথ হবে।
সংক্ষিপ্ততম পথ পেতে একাধিক উপায় আছে। কিন্তু আমাদের (k-1) পর্যন্ত সবচেয়ে ছোট পথটি খুঁজে বের করতে হবে।
কে-সংক্ষিপ্ত পথের জন্য অ্যালগরিদম
query= “””
MATCH(start: place{id:source}),*end: Place {Id:destination})
Call algo.kshortestPaths.stream(start,end,10, “distance”)
Yield nodeIDs, path costs, index
Return index.
[node in algo.getNodeByID(nodeId[1…..-1]) | node.id] aS,
Reduce (acc=0.0, cost in costs | acc+cost ) as total cost
“””
params= {“source”: Alex,Destination: “US”}
With driver.selection() as session:
Row session.run(query, params)
df = pd.DataFrame[dict(record) for record in rows])
pd.set_option(‘max_colwidth’, 100)
display(df) 

