সংলগ্নতা তালিকার প্রতিনিধিত্বের জন্য ডিজকস্ট্রার অ্যালগরিদম

এখানে একটি প্রদত্ত গ্রাফ G(V, E) রয়েছে যার সংলগ্ন তালিকা উপস্থাপনা রয়েছে এবং একটি উৎস শীর্ষবিন্দুও দেওয়া হয়েছে। ডিজকস্ট্রার অ্যালগরিদম গ্রাফ G এর অন্য কোনো শীর্ষ থেকে সোর্স শীর্ষবিন্দুর মধ্যে ন্যূনতম সংক্ষিপ্ততম পথ খুঁজে পেতে।

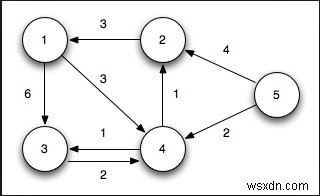
এই সমস্যাটি সমাধান করতে, আমরা দুটি তালিকা ব্যবহার করব। একটি হল শীর্ষবিন্দুগুলি সংরক্ষণ করা যা সংক্ষিপ্ত পথের গাছ হিসাবে বিবেচিত হয়েছে, এবং অন্যটি শীর্ষবিন্দুগুলিকে ধরে রাখবে যা এখনও বিবেচনা করা হয়নি৷ অ্যালগরিদমের প্রতিটি ধাপে, আমরা অবিবেচিত শীর্ষবিন্দু খুঁজে পাই এবং যার উৎস থেকে সর্বনিম্ন দূরত্ব রয়েছে।

পূর্বসূরী নোড ধরে রাখতে আরেকটি তালিকা ব্যবহার করা হয়। পূর্বসূরী নোড ব্যবহার করে, আমরা উৎস এবং গন্তব্য থেকে পথ খুঁজে পেতে পারি।

ডিজকস্ট্রার সংক্ষিপ্ততম পাথ অ্যালগরিদমের জটিলতা হল O(E লগ V) কারণ গ্রাফটি সংলগ্ন তালিকা ব্যবহার করে উপস্থাপন করা হয় . এখানে E হল প্রান্তের সংখ্যা, এবং V হল শীর্ষবিন্দুর সংখ্যা।

ইনপুট এবং আউটপুট

Input:
The adjacency list of the graph with the cost of each edge.

Output:
0 to 1, Cost: 3 Previous: 0
0 to 2, Cost: 5 Previous: 1
0 to 3, Cost: 4 Previous: 1
0 to 4, Cost: 6 Previous: 3
0 to 5, Cost: 7 Previous: 2
0 to 6, Cost: 7 Previous: 4

অ্যালগরিদম

dijkstraShortestPath(g : Graph, dist, prev, start : node)

ইনপুট - গ্রাফ g, দূরত্ব সঞ্চয় করার জন্য dist তালিকা, পূর্বসূরি নোডের জন্য পূর্বের তালিকা এবং শুরু শীর্ষবিন্দু।

আউটপুট - সূচনা থেকে অন্য সকল শীর্ষবিন্দুতে সংক্ষিপ্ততম পথ।

Begin
   for all vertices u in (V - start) do
      dist[u] := ∞
      prev[u] := φ
   done

   set dist[start] = 0 and prev[start] := φ

   for all node u in V do
      insert u into queue ‘Q’.
   done

   while Q is not empty do
      u := minimum element from Queue
      delete u from Q
      insert u into set S

      for each node v adjacent with node u do
         if dist[u]+cost(v) < dist[v] then
            dist[v] := dist[u]+cost(v)
            prev[v] := u
      done
   done
End

উদাহরণ

#include<iostream>
#include<set>
#include<list>
#include<algorithm>
using namespace std;

typedef struct nodes {
   int dest;
   int cost;
}node;

class Graph {
   int n;
   list<node> *adjList;
   private:
      void showList(int src, list<node> lt) {
         list<node> :: iterator i;
         node tempNode;

         for(i = lt.begin(); i != lt.end(); i++) {
            tempNode = *i;
            cout << "(" << src << ")---("<<tempNode.dest << "|"<<tempNode.cost<<") ";
         }
         cout << endl;
      }
   public:
      Graph() {
         n = 0;
      }

      Graph(int nodeCount) {
         n = nodeCount;
         adjList = new list<node>[n];
      }

      void addEdge(int source, int dest, int cost) {
         node newNode;
         newNode.dest = dest;
         newNode.cost = cost;
         adjList[source].push_back(newNode);
      }

      void displayEdges() {
         for(int i = 0; i<n; i++) {
            list<node> tempList = adjList[i];
            showList(i, tempList);
         }
      }

      friend void dijkstra(Graph g, int *dist, int *prev, int start);
};

void dijkstra(Graph g, int *dist, int *prev, int start) {
   int n = g.n;

   for(int u = 0; u<n; u++) {
      dist[u] = 9999;   //set as infinity
      prev[u] = -1;    //undefined previous
   }

   dist[start] = 0;   //distance of start is 0
   set<int> S;       //create empty set S
   list<int> Q;

   for(int u = 0; u<n; u++) {
      Q.push_back(u);    //add each node into queue
   }

   while(!Q.empty()) {
      list<int> :: iterator i;
      i = min_element(Q.begin(), Q.end());
      int u = *i; //the minimum element from queue
      Q.remove(u);
      S.insert(u); //add u in the set
      list<node> :: iterator it;

      for(it = g.adjList[u].begin(); it != g.adjList[u].end();it++) {
         if((dist[u]+(it->cost)) < dist[it->dest]) { //relax (u,v)
            dist[it->dest] = (dist[u]+(it->cost));
            prev[it->dest] = u;
         }
      }
   }
}

main() {
   int n = 7;
   Graph g(n);
   int dist[n], prev[n];
   int start = 0;

   g.addEdge(0, 1, 3);
   g.addEdge(0, 2, 6);
   g.addEdge(1, 0, 3);
   g.addEdge(1, 2, 2);
   g.addEdge(1, 3, 1);
   g.addEdge(2, 1, 6);
   g.addEdge(2, 1, 2);
   g.addEdge(2, 3, 1);
   g.addEdge(2, 4, 4);

   g.addEdge(2, 5, 2);
   g.addEdge(3, 1, 1);
   g.addEdge(3, 2, 1);
   g.addEdge(3, 4, 2);
   g.addEdge(3, 6, 4);
   g.addEdge(4, 2, 4);
   g.addEdge(4, 3, 2);
   g.addEdge(4, 5, 2);
   g.addEdge(4, 6, 1);
   g.addEdge(5, 2, 2);
   g.addEdge(5, 4, 2);
   g.addEdge(5, 6, 1);
   g.addEdge(6, 3, 4);
   g.addEdge(6, 4, 1);
   g.addEdge(6, 5, 1);

   dijkstra(g, dist, prev, start);

   for(int i = 0; i<n; i++)
      if(i != start)
         cout<<start<<" to "<<i<<", Cost: "<<dist[i]<<" Previous: "<<prev[i]<<endl;
}

আউটপুট

0 to 1, Cost: 3 Previous: 0
0 to 2, Cost: 5 Previous: 1
0 to 3, Cost: 4 Previous: 1
0 to 4, Cost: 6 Previous: 3
0 to 5, Cost: 7 Previous: 2
0 to 6, Cost: 7 Previous: 4