পাইথনে বুককেসের তাক ভর্তি করা

ধরুন আমাদের কাছে বইয়ের একটি ক্রম আছে − এখানে i-th বইটির পুরুত্বের বই[i][0] এবং উচ্চতার বই রয়েছে[i][1]। যদি আমরা এই বইগুলিকে বইয়ের তাকগুলিতে রাখতে চাই যার মোট প্রস্থের shelf_width আছে। যদি আমরা এই শেল্ফে রাখার জন্য কিছু বই বাছাই করি (যেমন তাদের পুরুত্বের যোগফল <=shelf_width), তাহলে বুককেসের অন্য স্তর তৈরি করুন যেখানে বুককেসের মোট উচ্চতা সর্বোচ্চ উচ্চতা দ্বারা বৃদ্ধি পেয়েছে। বই আমরা নামিয়ে রাখতে পারি। আমরা এই প্রক্রিয়াটি পুনরাবৃত্তি করব যতক্ষণ না আর কোন বই রাখার জন্য নেই। আমাদের মনে রাখতে হবে যে উপরের প্রক্রিয়ার প্রতিটি ধাপে, আমরা যে বইগুলি রাখি সেই ক্রমটি বইগুলির প্রদত্ত ক্রম অনুসারে একই ক্রম। এই পদ্ধতিতে তাক রাখার পরে আমাদের সর্বনিম্ন সম্ভাব্য উচ্চতা খুঁজে বের করতে হবে যা মোট বুকশেলফ হতে পারে। সুতরাং ইনপুট যদি হয় − [[1,1], [2,3], [2,3], [1,1], [1,1], [1,1], [1,2]] , এবং self_width =4,

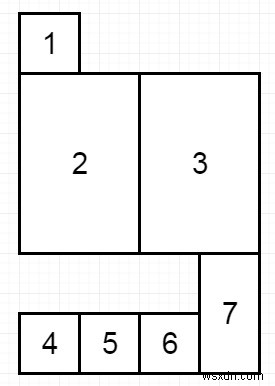
তাহলে আউটপুট হবে 6 কারণ 3টি শেল্ফের উচ্চতার সমষ্টি হল 1 + 3 + 2 =6৷ লক্ষ্য করুন যে বই নম্বর 2টি প্রথম শেলফে থাকতে হবে না৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি অ্যারে ডিপি তৈরি করুন যার আকার বইয়ের মতো, এবং অসীম ব্যবহার করে এটি পূরণ করুন
dp[0] :=বই[0,1]
আমার জন্য 1 থেকে বইয়ের দৈর্ঘ্য - 1
- curr_height :=0
- temp :=self_width
- j :=i
- যখন j>=0 এবং temp – বই[j, 0]>=0, do
  - curr_height :=বইয়ের সর্বোচ্চ [j, 1], curr_height
  - dp[i] :=dp[i] এর মিনিট, curr_height + (dp[j - 1] যদি j – 1>=0, অন্যথায় 0)
  - temp :=temp – বই[j, 0]
  - j 1 দ্বারা কমিয়ে দিন
ডিপির শেষ উপাদান ফেরত দিন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

class Solution(object):
   def minHeightShelves(self, books, shelf_width):
      """
      :type books: List[List[int]]
      :type shelf_width: int
      :rtype: int
      """
      dp = [float('inf') for i in range(len(books))]
      dp[0] = books[0][1]
      for i in range(1,len(books)):
         current_height = 0
         temp = shelf_width
         j = i
         while j>=0 and temp-books[j][0]>=0:
            current_height = max(books[j][1],current_height)
            dp[i] = min(dp[i],current_height +( dp[j-1] if j-1 >=0 else 0))
            temp-=books[j][0]
            j-=1
         #print(dp)
      return dp[-1]

ইনপুট

[[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]]
4