পাইথনে বাইনারি ট্রি কালারিং গেম

ধরুন একটি বাইনারি গাছে দুইজন খেলোয়াড় একটি পালা-ভিত্তিক খেলা খেলছে৷ আমাদের কাছে এই বাইনারি গাছের মূল এবং গাছে এন নোডের সংখ্যা রয়েছে। এখানে n বিজোড়, এবং প্রতিটি নোডের 1 থেকে n পর্যন্ত একটি স্বতন্ত্র মান রয়েছে। প্রথমে, প্রথম প্লেয়ারটি 1 <=x <=n সহ একটি মান x নাম দেয় এবং দ্বিতীয় খেলোয়াড় 1 <=y <=n সহ একটি মান y নাম দেয় এবং এটি একটি শর্ত ধারণ করে, যেমন y !=x। প্রথম প্লেয়ারটি নোডকে রঙ করে মান x লাল দিয়ে, এবং দ্বিতীয় প্লেয়ারটি নোডকে রঙ করে মান y নীল দিয়ে। এর পরে, খেলোয়াড়রা প্রথম খেলোয়াড় থেকে শুরু করে পালা করে। প্রতিটি পালাক্রমে, প্লেয়ার তাদের রঙের একটি নোড নেয় (প্লেয়ার 1 এর জন্য লাল, প্লেয়ার 2 এর জন্য নীল) এবং নির্বাচিত নোডের একটি বর্ণহীন প্রতিবেশীকে (হয় বাম বা ডান শিশু, বা নেওয়া নোডের পিতামাতা) রঙ করে। যদি এবং শুধুমাত্র যদি একজন খেলোয়াড় এইভাবে একটি নোড নিতে না পারে, তবে তাদের অবশ্যই তাদের পালা পাস করতে হবে। যদি উভয় খেলোয়াড় তাদের পালা পাস করে, গেমটি শেষ হয়ে যাবে, এবং বিজয়ী হবেন সেই খেলোয়াড় যে আরও নোডগুলিকে রঙ করেছে৷

ধরুন আমরা দ্বিতীয় খেলোয়াড়। খেলায় জয় নিশ্চিত করার জন্য যদি এমন একটি y বেছে নেওয়া সম্ভব হয়, তাহলে সত্যে ফিরে আসুন। যদি এটি সম্ভব না হয়, মিথ্যা ফেরত দিন।

তাই গাছটি যদি −

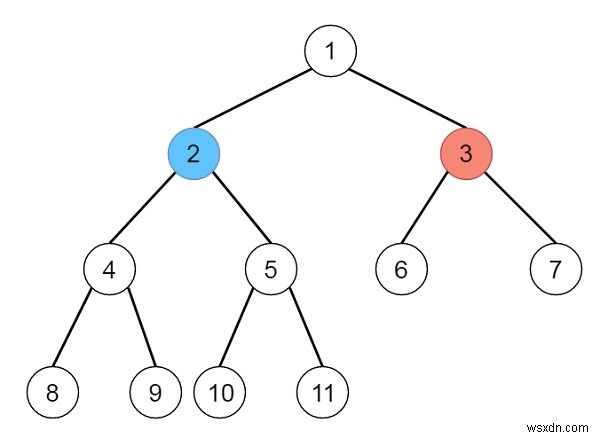
এবং n হল 11 এবং x হল 3, তাহলে আউটপুট সত্য হবে, কারণ দ্বিতীয় প্লেয়ারটি 2 মান সহ নোড নিতে পারে

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• সমাধান() নামক একটি পদ্ধতির সংজ্ঞা দিন, এটি নোড নেবে, x, l এবং r, l এবং r প্রাথমিকভাবে মিথ্যা, এটি নীচের মত কাজ করবে -

• যদি নোড উপস্থিত না থাকে, তাহলে ফিরে আসুন এবং প্রস্থান করুন

• যদি l সত্য হয়, তাহলে লেফটভ্যাল 1 দ্বারা বাড়ান, অন্যথায় যখন r সত্য হয়, তাহলে ডানভাল 1 দ্বারা বাড়ান

• যদি নোডের মান x হয়, তাহলে সমাধান কল করুন (নোডের বামে, x, সত্য, মিথ্যা) এবং কল সমাধান (নোডের ডানদিকে, x, মিথ্যা, সত্য)

• অন্যথায় কল সল্ভ (নোডের বামে, x, l, r) এবং কল সল্ভ (নোডের ডানদিকে, x, l, r)

• মূল পদ্ধতিটি হবে −

  এর মত

• nodeToX :=0, leftVal :=0, rightVal :=0

• কল সমাধান(root, x, false, false)

• nodeToX :=n – leftVal – rightVal – 1

• temp :=rightVal, nodeToX এবং leftVal এর সর্বাধিক

• মিথ্যা ফেরত দিন যদি (nodeToX + leftVal + rightVal – (2*temp)>=0), অন্যথায় সত্য

উদাহরণ(পাইথন)

আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right
def insert(temp,data):
   que = []
   que.append(temp)
   while (len(que)):
      temp = que[0]
      que.pop(0)
      if (not temp.left):
         if data is not None:
            temp.left = TreeNode(data)
         else:
            temp.left = TreeNode(0)
         break
      else:
         que.append(temp.left)
      if (not temp.right):
         if data is not None:
            temp.right = TreeNode(data)
         else:
            temp.right = TreeNode(0)
         break
      else:
         que.append(temp.right)
def make_tree(elements):
   Tree = TreeNode(elements[0])
   for element in elements[1:]:
      insert(Tree, element)
   return Tree
class Solution(object):
   def btreeGameWinningMove(self, root, n, x):
      self.nodeToX = 0
      self.leftVal = 0
      self.rightVal = 0
      self.solve(root,x)
      self.nodeToX = n - self.leftVal - self.rightVal - 1
      temp = max(self.rightVal,max(self.nodeToX,self.leftVal))
      return not (self.nodeToX + self.leftVal + self.rightVal - (2*temp)>=0)
   def solve(self,node,x,l= False,r = False):
      if not node:
         return
      if l:
         self.leftVal+=1
      elif r:
         self.rightVal+=1
      if node.data == x:
         self.solve(node.left,x,True,False)
         self.solve(node.right,x,False,True)
      else:
         self.solve(node.left,x,l,r)
         self.solve(node.right,x,l,r)
ob = Solution()
root = make_tree([1,2,3,4,5,6,7,8,9,10,11])
print(ob.btreeGameWinningMove(root, 11, 3))

ইনপুট

[1,2,3,4,5,6,7,8,9,10,11]
11
3

আউটপুট

true