পাইথনে অয়লার সার্কিট তৈরি করতে ন্যূনতম প্রান্ত যোগ করতে হবে

ধরুন আমাদের b সংখ্যার নোড এবং বেশ কয়েকটি প্রান্তের একটি অনির্দেশিত গ্রাফ আছে; আমাদের এই গ্রাফে অয়লার সার্কিট তৈরির জন্য প্রয়োজনীয় ন্যূনতম প্রান্তগুলি খুঁজে বের করতে হবে৷

সুতরাং, যদি ইনপুট মত হয়

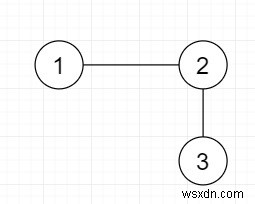
তাহলে আউটপুট হবে 1.

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি ফাংশন dfs() সংজ্ঞায়িত করুন। এর জন্য g, visit, odd_vert, ডিগ্রি, comp, v
ভিজিট[v] :=1
যদি ডিগ্রি[v] মোড 2 1 এর মত হয়, তাহলে
- odd_vert[comp] :=odd_vert[comp] + 1
আপনার জন্য 0 থেকে g[v] এর আকারের মধ্যে, করুন
- যদি ভিজিট[u] 0 এর মত হয়, তাহলে
  - dfs(g, visit, odd_vert, degree, comp, u)
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
g :=n+1 ফাঁকা তালিকার একটি তালিকা
e :=একটি নতুন তালিকা
:=একটি নতুন তালিকা
ডিগ্রী :=আকারের নতুন তালিকা (n + 1) এবং 0 দিয়ে পূরণ করুন
ভিজিট করুন :=আকারের নতুন তালিকা (n + 1) এবং 0 দিয়ে পূরণ করুন
odd_vert :=আকারের নতুন তালিকা (n + 1) এবং পূরণ করুন
0 সহ
আমি 0 থেকে m রেঞ্জের জন্য, কর
- g[s[i]] এর শেষে d[i] ঢোকান
- g[d[i]] এর শেষে s[i] ঢোকান
- ডিগ্রী[s[i]] :=ডিগ্রী[s[i]] + 1
- ডিগ্রী[d[i]] :=ডিগ্রী[d[i]] + 1
উত্তর :=0, comp :=0
1 থেকে n + 1 রেঞ্জের জন্য,
- যদি ভিজিট[i] 0 এর মত হয়, তাহলে
  - comp :=comp + 1
  - dfs(g, visit, odd_vert, degree, comp, i)
  - যদি odd_vert[comp] 0 এর মত হয়, তাহলে
    - e এর শেষে comp ঢোকান
  - অন্যথায়,
    - o-এর শেষে comp ঢোকান
যদি o এর সাইজ 0 এর মত হয় এবং e এর সাইজ 1 এর মত হয়, তাহলে
- রিটার্ন 0
যদি o এর আকার 0 এর সমান হয়, তাহলে
- ই এর রিটার্ন সাইজ
যদি e-এর আকার 0 এর মতো না হয়, তাহলে
- উত্তর :=ans + e এর আকার
আমি 0 থেকে o আকারের রেঞ্জের জন্য, কর
- উত্তর :=ans + odd_vert[i] / 2 (শুধুমাত্র পূর্ণসংখ্যা অংশ নিন)
উত্তর ফেরত দিন

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def dfs(g, visit, odd_vert, degree, comp, v):
   visit[v] = 1
   if (degree[v] % 2 == 1):
      odd_vert[comp] += 1
   for u in range(len(g[v])):
      if (visit[u] == 0):
         dfs(g, visit, odd_vert, degree, comp, u)
def solve(n, m, s, d):
   g = [[] for i in range(n + 1)]
   e = []
   o = []
   degree = [0] * (n + 1)
   visit = [0] * (n + 1)
   odd_vert = [0] * (n + 1)
   for i in range(m):
      g[s[i]].append(d[i])
      g[d[i]].append(s[i])
      degree[s[i]] += 1
      degree[d[i]] += 1
   ans = 0
   comp = 0
   for i in range(1, n + 1):
      if (visit[i] == 0):
         comp += 1
         dfs(g, visit, odd_vert, degree, comp, i)
         if (odd_vert[comp] == 0):
            e.append(comp)
         else:
            o.append(comp)
   if (len(o) == 0 and len(e) == 1):
      return 0
   if (len(o) == 0):
      return len(e)
   if (len(e) != 0):
      ans += len(e)
   for i in range(len(o)):
      ans += odd_vert[i] // 2
   return ans
b = 3
a = 2
source = [ 1, 2 ]
destination = [ 2, 3]
print(solve(b, a, source, destination))

ইনপুট

b = 3 a = 2 source = [ 1, 2 ] destination = [ 2, 3]