পাইথনে একটি বন সংযোগ করার জন্য প্রোগ্রাম

ধরুন আমরা একটি সংলগ্ন তালিকা হিসাবে গ্রাফ আছে. এই গ্রাফটি আসলে বিচ্ছিন্ন গাছের একটি সেট। আমাদের বনে একটি নির্দিষ্ট সংখ্যক প্রান্ত যোগ করতে হবে যাতে এটি একটি একক গাছে পরিণত হয়। আমাদের যেকোনো দুটি নোডের মধ্যে দীর্ঘতম পথের সম্ভাব্য ন্যূনতম দূরত্ব ফিরিয়ে দিতে হবে। সুতরাং, যদি ইনপুট মত হয়

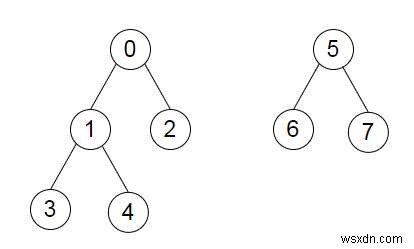
তাহলে আউটপুট হবে 4.

আমরা প্রান্তটি 0 −> 5 যোগ করতে পারি। তারপর, দীর্ঘতম পথটি 3 −> 1 −> 0 −> 5 −> 7 বা 4 −> 1 −> 0 −> 5 −> 7 হতে পারে; এবং দিক উল্টানো সঙ্গে এই পাথ. তাই আমরা দূরত্ব 4 ফেরত দিই।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• দেখা হয়েছে :=একটি নতুন সেট

• dic :=গ্রাফ

• একটি ফাংশন treeDepth() সংজ্ঞায়িত করুন। এটি নোড নেবে।

  • ret :=0

  • একটি ফাংশন dfs1() সংজ্ঞায়িত করুন। এটি নোড নেবে, পিতামাতা৷

    ৷

    • দেখা সেটে একটি নোড যোগ করুন

    • best2 :=একটি খালি মিনিট গাদা গঠন

    • dic[নোড]-এ প্রতিটি nxt-এর জন্য করুন

      • যদি nxt অভিভাবক হিসাবে একই না হয়, তাহলে

        • push(dfs1(nxt, node) + 1) best2

          -এ

      • যদি len(best2)> 2, তাহলে

        • পপ ফ্রম হিপ(সেরা2)

      • যদি best2 খালি হয়, তাহলে

        • রিটার্ন 0

      • ret :=ret এর সর্বোচ্চ, best2 এর সমস্ত উপাদানের যোগফল

      • সর্বোচ্চ 2

        ফেরত দিন

    • dfs1(নোড, নাল)

    • রিটার্ন রিটার্ন

• মূল পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -

• ret :=0, opt :=একটি নতুন তালিকা, sing :=0

  • 0 থেকে গ্রাফের আকারের মধ্যে নোডের জন্য, করুন

    • যদি নোড দেখা যায়, তাহলে

      • পরবর্তী পুনরাবৃত্তির জন্য যান

    • res :=treeDepth(নোড)

    • sing :=সর্বাধিক গাওয়া, রেস

    • অপ্ট

      এর শেষে (res / 2) এর সিলিং ঢোকান

  • যদি অপ্টের আকার <=1, তারপর

    • ফিরতি গান

  • mx :=সর্বাধিক অপট

  • আমি 0 থেকে অপ্টের আকারের মধ্যে, কর

    • যদি opt[i] mx এর মত হয়, তাহলে

      • opt[i] :=opt[i] − 1

      • লুপ থেকে বেরিয়ে আসুন

  • আমি 0 থেকে অপ্টের আকারের মধ্যে, কর

    • opt[i] :=opt[i] + 1

  • high2 :=অপ্ট থেকে বৃহত্তম 2 উপাদান।

  • সর্বাধিক যোগফল (উচ্চ2) ফেরত দিন এবং গান করুন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

import heapq, math
class Solution:
   def solve(self, graph):
      seen = set()
      dic = graph
      def treeDepth(node):
         self.ret = 0
         def dfs1(node, parent):
            seen.add(node)
            best2 = []
            for nxt in dic[node]:
               if nxt != parent:
                  heapq.heappush(best2, dfs1(nxt, node) + 1)
                  if len(best2) > 2:
                     heapq.heappop(best2)
            if not best2:
               return 0
            self.ret = max(self.ret, sum(best2))
            return max(best2)
         dfs1(node, None)
         return self.ret
      ret = 0
      opt = []
      sing = 0
      for node in range(len(graph)):
         if node in seen:
            continue
         res = treeDepth(node)
         sing = max(sing, res)
         opt.append(int(math.ceil(res / 2)))
      if len(opt) <= 1:
         return sing
      mx = max(opt)
      for i in range(len(opt)):
         if opt[i] == mx:
            opt[i] −= 1
            break
         for i in range(len(opt)):
            opt[i] += 1
         high2 = heapq.nlargest(2, opt)
         return max(sum(high2), sing)
ob = Solution()
graph = [
   [1, 2],
   [0,3,4],
   [0],
   [1],
   [1],
   [6,7],
   [5],
   [5]
]
print(ob.solve(graph))

ইনপুট

graph = [
   [1, 2],
   [0,3,4],
   [0],
   [1],
   [1],
   [6,7],
   [5],
   [5]
]

আউটপুট

4