ধরুন আমাদের দুটি N X M বাইনারি ম্যাট্রিস A এবং B রয়েছে। একটি একক অপারেশনে, আমরা একটি সাব-ম্যাট্রিক্স (অন্তত 2x2) নির্বাচন করতে পারি এবং কোণার উপাদানগুলির (ফ্লিপ বিট) সমতা রূপান্তর করতে পারি। পরিশেষে, আমাদের পরীক্ষা করতে হবে যে কোনো সংখ্যক অপারেশন করে ম্যাট্রিক্স A কে B তে রূপান্তর করা যায় কি না।
সুতরাং, যদি ইনপুট মত হয়
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
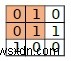
তাহলে আউটপুট True হবে কারণ আমরা mat2 পেতে mat1-এ উপরের বাম বর্গাকার সাব-ম্যাট্রিক্সের (2x2) উপর অপারেশন করতে পারি।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- সারি :=ম্যাট1 এর সারি গণনা
- কলাম :=ম্যাট1 এর কলাম সংখ্যা
- আমি 1 থেকে সারি - 1 রেঞ্জের জন্য, কর
- 1 থেকে কলাম - 1 পর্যন্ত j-এর জন্য
- করুন
- যদি mat1[i, j] mat2[i, j] এর মত না হয়, তাহলে
- mat1[i, j] :=mat1[i, j] XOR 1
- mat1[0, 0] :=mat1[0, 0] XOR 1
- mat1[0, j] :=mat1[0, j] XOR 1
- mat1[i, 0] :=mat1[i, 0] XOR 1
- যদি mat1[i, j] mat2[i, j] এর মত না হয়, তাহলে
- করুন
- আমি 0 থেকে সারি - 1 এর মধ্যে, কর
- 0 থেকে কলাম - 1 পর্যন্ত j এর জন্য, করুন
- যদি mat1[i, j] mat2[i, j] এর মত না হয়, তাহলে
- মিথ্যে ফেরত দিন
- যদি mat1[i, j] mat2[i, j] এর মত না হয়, তাহলে
- 0 থেকে কলাম - 1 পর্যন্ত j এর জন্য, করুন
- সত্য ফেরান
উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
def সমাধান(mat1, mat2):row =len(mat1) কলাম =len(mat1[0]) রেঞ্জে i এর জন্য(1, সারি):j এর জন্য রেঞ্জ(1, কলাম):যদি mat1[i ][j] !=mat2[i][j]:mat1[i][j] ^=1 mat1[0][0] ^=1 mat1[0][j] ^=1 mat1[i][0 ] ^=1 রেঞ্জে i এর জন্য (সারি):রেঞ্জে j এর জন্য (কলাম):যদি mat1[i][j] !=mat2[i][j]:রিটার্ন ফলস রিটার্ন Truemat1 =[ [1, 0, 0 ], [1, 0, 1], [1, 0, 0]]mat2 =[ [0, 1, 0], [0, 1, 1], [1, 0, 0]]মুদ্রণ(সমাধান(mat1) , mat2))
ইনপুট
<প্রে>[ [1, 0, 0], [1, 0, 1], [1, 0, 0]], [ [0, 1, 0], [0, 1, 1], [1, 0 , 0]]আউটপুট
সত্য


