এক্সপ্রেশন ট্রি হলো এমন ট্রি যেখানে লিফ নোডগুলোর মান থাকে যেগুলো অপারেট করা হবে, এবং ইন্টারন্যাল নোডগুলো অপারেটর ধারণ করে যার ওপর লিফ নোড অপারেট হবে।
উদাহরণ: 4 + ((7 + 9) * 2) এর এক্সপ্রেশন ট্রি হবে -
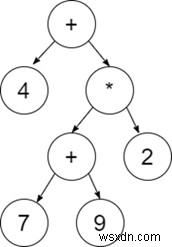
সমস্যা সমাধানের পদ্ধতি
এক্সপ্রেশন ট্রি নির্মাণের জন্য সাধারণত Stack Data Structure ব্যবহার করা হয়। প্রাথমিকভাবে দেওয়া পোস্টফিক্স এক্সপ্রেশনের ওপর ইটারেট করে নিচের ধাপগুলো অনুসরণ করা হয়:
- যদি এক্সপ্রেশনতে অপারেন্ড (operand) পাওয়া যায়, তবে সেটাকে স্টকে পুশ করুন। এটি এক্সপ্রেশন ট্রির রুট হবে।
- যদি অপারেটর (operator) দুটি ভ্যালু পায় এক্সপ্রেশনতে, তবে সেগুলো এক্সপ্রেশন ট্রিতে এর চাইল্ড হিসেবে যোগ করুন এবং কারেন্ট নোডে পুশ করুন।
- দেওয়া এক্সপ্রেশন पूरा না হওয়া পর্যন্ত ধাপ ১ এবং ২ রিপিট করুন।
উদাহরণ
class stack:
def __init__(self):
self.arr = []
def push(self, data):
self.arr.append(data)
def pop(self):
try:
return self.arr.pop(-1)
except:
pass
def top(self):
try:
return self.arr[-1]
except:
pass
def size(self):
return len(self.arr)
# এক্সপ্রেশন ট্রির জন্য নোড ক্লাস
class node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# এক্সপ্রেশন ট্রি ক্লাস
class exp_tree:
def __init__(self, postfix_exp):
self.exp = postfix_exp
self.root = None
self.createTree(self.exp)
def isOperator(self, char):
optr = ["+", "-", "*", "/", "^"]
if char in optr:
return True
return False
def createTree(self, exp):
s = stack()
# অপারেটর নোড স্টোর যাদের চাইল্ড NULL
self.root = node(exp[-1])
# পোস্টফিক্স এক্সপ্রেশনের লাস্ট ক্যারেক্টার সবসময় অপারেটর
s.push(self.root)
# বাকি পোস্টফিক্স এক্সপ্রেশনে ট্রাভার্স
for i in "".join(reversed(exp[:-1])):
curr_node = s.top()
if not curr_node.right:
# কারেন্ট নোডের রাইট নোড NULL হলে
temp = node(i)
curr_node.right = temp
if self.isOperator(i):
s.push(temp)
else: # কারেন্ট নোডের লেফট নোড NULL হলে
temp = node(i)
curr_node.left = temp
# কারেন্ট নোডের কোনো চাইল্ড NULL না হলে
s.pop() # কারেন্ট স্টকে থেকে পপ
if self.isOperator(i):
s.push(temp)
def inorder(self, head):
# এক্সপ্রেশন ট্রির ইনঅর্ডার ট্রাভার্সাল
# ইনঅর্ডার = লেফট, রুট, রাইট
if head.left:
self.inorder(head.left)
print(head.data, end=" ")
if head.right:
self.inorder(head.right)
def infixExp(self):
# ইনঅর্ডার ট্রাভার্সাল ইনফিক্স এক্সপ্রেশন দেয়
self.inorder(self.root)
print()
if __name__ == "__main__":
postfixExp = "ab ef*g*-"
et = exp_tree(postfixExp)
et.infixExp()
উপরের কোড রান করলে আউটপুট আসবে:
আউটপুট
(a + b - e * f * g)
ব্যাখ্যা:
দেওয়া এক্সপ্রেশন থেকে ট্রি নির্মাণ করলে আউটপুট জেনারেট হবে যেন অপারেন্ড নোডের রুট হয় এবং বাকি নম্বরগুলো এক্সপ্রেশন ট্রির চাইল্ড নোড হয়।
