পাইথন ব্যবহার করে একটি বাইনারি গ্রিড সাজানোর জন্য সর্বনিম্ন অদলবদল খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি n x n বাইনারি ম্যাট্রিক্স আছে। আমরা এটিতে একটি অপারেশন করতে পারি যেমন, এক ধাপে আমরা দুটি সংলগ্ন সারি নির্বাচন করি এবং তাদের অদলবদল করি। আমাদের প্রয়োজনীয় ন্যূনতম অদলবদলের সংখ্যা গণনা করতে হবে, যাতে ম্যাট্রিক্সের প্রধান কর্ণের উপরের সমস্ত নোড 0 হয়। যদি এই ধরনের কোন সমাধান না থাকে, তাহলে -1 ফেরত দিন।

সুতরাং, যদি ইনপুট মত হয়

0	1	0
0	1	1
1	0	0

তাহলে আউটপুট হবে 2 কারণ −

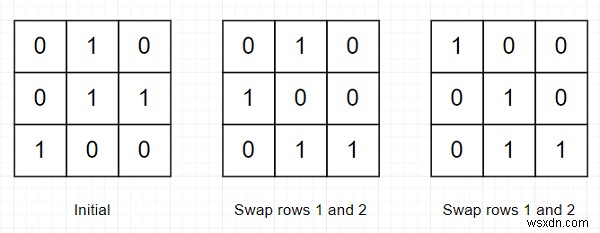
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব:

n :=ম্যাট্রিক্সের সারি গণনা
m :=n আকারের একটি অ্যারে তৈরি করুন এবং n
দিয়ে পূরণ করুন
আমি 0 থেকে n - 1 রেঞ্জের জন্য, করুন
- j-এর জন্য n-1 থেকে 0 রেঞ্জের মধ্যে, 1 দ্বারা হ্রাস করুন, করুন
  - যদি ম্যাট্রিক্স[i, j] 1 এর মত হয়, তাহলে
    - m[i] :=n-j-1
    - লুপ থেকে বেরিয়ে আসুন
t :=0, উত্তর :=0
আমি 0 থেকে n - 1 রেঞ্জের জন্য, করুন
- t :=t + 1
- পতাকা :=মিথ্যা
- j-এর জন্য i থেকে n - 1 পরিসরে, do
  - যদি m[j]>=n-t, তাহলে
    - ans :=ans + j-i
    - পতাকা :=সত্য
    - লুপ থেকে বেরিয়ে আসুন
- যদি পতাকা মিথ্যা হয়, তাহলে
  - রিটার্ন -1
- m[সূচী i+1 থেকে j] m দ্বারা m[সূচী i থেকে j-1]
  আপডেট করুন
উত্তর ফেরত দিন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

def solve(matrix):
   n = len(matrix)
   m = [n] * n
   for i in range(n):
      for j in range(n-1,-1,-1):
         if matrix[i][j] == 1:
            m[i] = n-j-1
            break
   t,ans = 0,0
   for i in range(n):
      t += 1
      flag = False
      for j in range(i,n):
         if m[j] >= n-t:
            ans += j-i
            flag = True
            break
      if not flag: return -1
      m[i+1:j+1] = m[i:j]
   return ans
matrix = [[0,1,0],[0,1,1],[1,0,0]]
print(solve(matrix))

ইনপুট

[[0,1,0],[0,1,1],[1,0,0]]