পাইথনের প্রতিটি অবস্থানে পৌঁছানোর জন্য একটি দাবা অংশের জন্য ন্যূনতম সংখ্যক চাল খুঁজে বের করার প্রোগ্রাম

ধরুন, আমাদের একটি দাবাবোর্ড এবং একটি বিশেষ নাইট পিস K আছে, যা বোর্ডের মধ্যে একটি L আকারে চলে। যদি টুকরাটি অবস্থানে থাকে (x1, y1) এবং যদি এটি (x2, y2) এ চলে যায় তবে গতিকে x2 =x1 ± a হিসাবে বর্ণনা করা যেতে পারে; y2 =y1 ± b বা x2 =x1 ± b; y2 =y1 ± a; যেখানে a এবং b পূর্ণসংখ্যা। দাবা বোর্ডে অবস্থান থেকে (0, 0) অবস্থানে পৌঁছাতে (n-1, n-1) পৌঁছানোর জন্য সেই দাবা অংশটির জন্য আমাদের সর্বনিম্ন সংখ্যক চাল খুঁজে বের করতে হবে। যদি একটি অবস্থান পৌঁছানো সম্ভব না হয়, এটি -1 চিহ্নিত করা হয়, অন্যথায়, চালের সংখ্যা ফেরত দেওয়া হয়। আমরা n – 1 লাইনের আউটপুট প্রিন্ট করব, যেখানে প্রতিটি লাইন i তে n − 1 পূর্ণসংখ্যা থাকবে যা প্রতিটি j-এর জন্য অংশটিকে ন্যূনতম কত নড়াচড়া করতে হবে তা বর্ণনা করে।

সুতরাং, যদি ইনপুট n =6 এর মত হয়, তাহলে আউটপুট হবে

5  4  3  2  5
4 -1  2 -1 -1
3  2 -1 -1 -1
2 -1 -1 -1 -1
5 -1 -1 -1  1

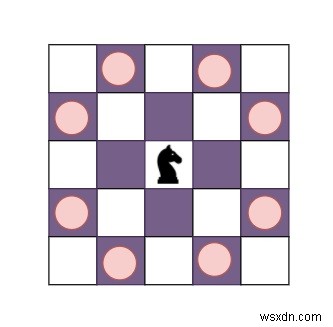
5x5 চেসবোর্ডে (3, 3) অবস্থানে থাকলে নাইটের জন্য সম্ভাব্য চাল।

আউটপুটের প্রথম লাইনে (1,1) থেকে (1,5) অবস্থানে পৌঁছানোর জন্য টুকরাটির ন্যূনতম সংখ্যক চালনা রয়েছে। পরপর লাইন একইভাবে প্রতিটি নিজ নিজ I এবং j মানের জন্য সর্বনিম্ন নড়াচড়ার সংখ্যা বর্ণনা করে।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি ফাংশন সংজ্ঞায়িত করুন path_search()। এটি i, j, n

  লাগবে

  • temp_list :=জোড়া দিয়ে শুরু করা একটি নতুন মানচিত্র (-1, -1)

  • queue_positional :=জোড়া দিয়ে শুরু করা একটি নতুন তালিকা (0, 0)

  • ver :=[(i, j) ,(-i, j) ,(i, -j) ,(-i, -j),(j, i),(j, -i),(-j, i ),(-j, -i) ]

  • যখন queue_positional> 0 এর সাইজ, do

    • current_element :=queue_positional

      থেকে প্রথম উপাদান মুছে দিন

    • ver এর প্রতিটি উপাদানের জন্য, করুন

      • x :=উপাদান[0] + বর্তমান_উপাদান[0]

      • y :=উপাদান[1] + বর্তমান_উপাদান[1]

      • যদি -1

        • temp_list[x, y] :=বর্তমান_উপাদান

        • queue_positional

          এর শেষে জোড়া (x, y) সন্নিবেশ করান

        • যদি x n - 1 এর মত হয় এবং y n - 1 এর মত হয়, তাহলে

          • count_var :=1

          • যখন temp_list[x,y] (0, 0), do

            এর মতো নয়

            • count_var :=count_var + 1

            • x, y :=temp_list[x,y]

          • ফিরতি গণনা_ভার

  • রিটার্ন -1

প্রধান ফাংশন/পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -

• বোর্ড :=-1

  দিয়ে শুরু করা একটি নতুন মানচিত্র

• 1 থেকে n রেঞ্জের জন্য, করুন

  • 1 থেকে i রেঞ্জের মধ্যে j এর জন্য, করুন

    • যদি বোর্ড[i, j] -1 এর মত হয়, তাহলে

      • বোর্ড[i, j] :=path_search(i, j, n)

      • বোর্ড[j, i] :=বোর্ড[i, j]

    • যদি (n - 1) mod i 0 এর মত হয়, তাহলে

      • বোর্ড[i, i] :=(n - 1) / i

• 1 থেকে n রেঞ্জের জন্য, করুন

  • 1 থেকে n - 1 পরিসরে j এর জন্য, করুন

    • প্রিন্ট (বোর্ড[i, j])

  • মুদ্রণ (বোর্ড[i, n - 1])

সোর্স কোড (পাইথন)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

from collections import defaultdict
def path_search(i, j, n):
   temp_list = defaultdict(lambda: (-1,-1))
   queue_positional = [(0, 0)]
   ver = [(i, j), (-i, j), (i, -j), (-i, -j), (j, i), (j, -i), (-j, i), (-j, -i)]
   while len(queue_positional) > 0:
      current_element = queue_positional.pop(0)
      for element in ver:
         x = element[0] + current_element[0]
         y = element[1] + current_element[1]
         if -1 < x < n and -1 < y < n and temp_list[x, y] == (-1,-1):
            temp_list[x, y] = current_element
            queue_positional.append((x, y))
            if x == n - 1 and y == n - 1:
               count_var = 1
               while temp_list[x,y]!=(0,0):
                  count_var += 1
                  x, y = temp_list[x,y]
               return count_var
   return -1

def solve(n):
   board = defaultdict(lambda: -1)
   for i in range(1, n):
      for j in range(1, i):
         if board[i, j] == -1:
            board[i, j] = path_search(i, j, n)
            board[j, i] = board[i, j]
      if (n - 1) % i == 0:
         board[i, i] = (n - 1) / i

   for i in range(1, n):
      for j in range(1, n - 1):
         print(int(board[i, j]), end = ' ')
   print(int(board[i, n - 1]))

solve(6)

ইনপুট

6

আউটপুট

5  4  3  2  5
4 -1  2 -1 -1
3  2 -1 -1 -1
2 -1 -1 -1 -1
5 -1 -1 -1  1