পাইথনে প্রথম থেকে শেষ নোড পর্যন্ত সীমাবদ্ধ পথের সংখ্যা খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি অনির্দেশিত ওজনযুক্ত সংযুক্ত গ্রাফ আছে। গ্রাফটিতে n নোড রয়েছে এবং সেগুলি 1 থেকে n পর্যন্ত লেবেলযুক্ত। শুরু থেকে শেষ পর্যন্ত একটি পথ হল [z0, z1, z2, ..., zk] এর মতো নোডগুলির একটি ক্রম এখানে z0 হল স্টার্ট নোড এবং zk হল শেষ নোড এবং zi এবং zi+1 এর মধ্যে একটি প্রান্ত রয়েছে যেখানে 0 <=i <=k-1. পথের দূরত্ব হল পথের প্রান্তে থাকা ওজনের মানের সমষ্টি। ধরুন dist(x) নোড n এবং নোড x থেকে সবচেয়ে কম দূরত্ব নির্দেশ করে। একটি সীমাবদ্ধ পাথ হল একটি বিশেষ পাথ যা সেই dist(zi)> dist(zi+1) যেখানে 0 <=i <=k-1 কে সন্তুষ্ট করে। সুতরাং, আমাদের নোড 1 থেকে নোড n পর্যন্ত সীমাবদ্ধ পথের সংখ্যা খুঁজে বের করতে হবে। উত্তরটি খুব বড় হলে উত্তর মডিউল 10^9 + 7.

সুতরাং, যদি ইনপুট মত হয়

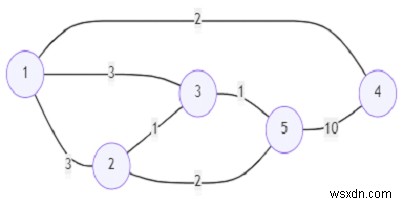
তাহলে আউটপুট 3 হবে কারণ তিনটি সীমাবদ্ধ পথ রয়েছে (1,2,5), (1,2,3,5), (1,3,5)।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• গ্রাফ :=প্রদত্ত প্রান্ত তালিকা থেকে তৈরি গ্রাফের সংলগ্ন তালিকা

• পাথ :=আকারের একটি অ্যারে (n+1) এবং 0

  দিয়ে পূর্ণ

• পথ [n] :=1

• dists :=আকারের একটি অ্যারে (n+1) এবং -1

  দিয়ে পূর্ণ

• q :=একটি সারি, এবং প্রথমে (0, n) সন্নিবেশ করুন

• q খালি না থাকার সময়, করুন

  • (dist, node) :=q এর সামনের উপাদান এবং q

    থেকে সরিয়ে দিন

  • যদি dists[নোড] -1 এর মত না হয়, তাহলে

    • পরবর্তী পুনরাবৃত্তির জন্য যান

  • dists[নোড] :=dist

  • প্রতিটি সংলগ্ন নোড v এবং গ্রাফ[নোড] এর ওজন w এর জন্য, করুন

    • যদি দূরত্ব[v] -1 এর মত হয়, তাহলে

      • q

        -এ (dist + w, v) সন্নিবেশ করান

    • অন্যথায় যখন dists[v]

      • পাথ[নোড] :=পাথ[নোড] + পাথ[v]

  • যদি নোড 1 এর মত হয়, তাহলে

    • রিটার্ন পাথ [নোড] মোড 10^9+7

• রিটার্ন 0

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

from collections import defaultdict
from heapq import heappop, heappush
def solve(n, edges):
   graph = defaultdict(dict)
   for u, v, w in edges:
      graph[u][v] = w
      graph[v][u] = w

   paths = [0] * (n+1)
   paths[n] = 1
   dists = [-1] * (n+1)
   q = [(0, n)]

   while q:
      dist, node = heappop(q)
      if dists[node] != -1:
         continue

      dists[node] = dist
      for v, w in graph[node].items():
         if dists[v] == -1:
            heappush(q, (dist + w, v))
         elif dists[v] < dists[node]:
            paths[node] += paths[v]

      if node == 1:
         return paths[node] % (10**9 + 7)

   return 0

n = 5
edges = [(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)]
print(solve(n, edges))

ইনপুট

5,[(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)]

আউটপুট

3