পাইথনে Prim-এর অ্যালগরিদম ব্যবহার করে একটি MST খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি গ্রাফ দেওয়া হয়েছে এবং সেই গ্রাফ থেকে 'মিনিমাম স্প্যানিং ট্রি' (MST) বের করতে বলা হয়েছে। একটি গ্রাফের একটি MST হল একটি ওজনযুক্ত গ্রাফের একটি উপসেট যেখানে সমস্ত শীর্ষবিন্দু উপস্থিত এবং সংযুক্ত থাকে এবং উপসেটে কোনো চক্র থাকে না। MST-কে সর্বনিম্ন বলা হয় কারণ MST-এর মোট প্রান্তের ওজন গ্রাফ থেকে সর্বনিম্ন সম্ভব। তাই, এখানে আমরা Prim-এর MST অ্যালগরিদম ব্যবহার করি এবং একটি প্রদত্ত গ্রাফ থেকে MST-এর মোট প্রান্তের ওজন বের করি।

সুতরাং, যদি ইনপুট মত হয়

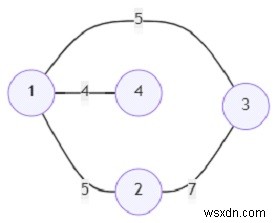
, শীর্ষবিন্দুর সংখ্যা (n) 4, এবং শুরু শীর্ষবিন্দু (s) =3, তাহলে আউটপুট হবে 14।

এই গ্রাফ থেকে MST হবে এই −

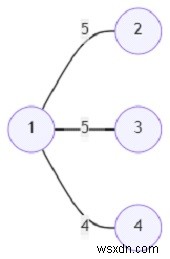
এই MST এর মোট প্রান্ত ওজন হল 14.

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি ফাংশন mst_find() সংজ্ঞায়িত করুন। এর জন্য G, s
  লাগবে
  • দূরত্ব :=মান ঋণাত্মক অসীমতার সাথে শুরু করা G আকারের একটি নতুন তালিকা
  • দূরত্ব[গুলি] :=0
  • itr :=False মান সহ শুরু করা G আকারের একটি নতুন তালিকা
  • c :=0
  • যদিও সত্য, কর
    • min_weight :=অসীম
    • m_idx :=-1
    • আমি 0 থেকে G এর আকারের মধ্যে, কর
      • যদি itr[i] False এর মত হয়, তাহলে
        • যদি দূরত্ব[i]
        • min_weight :=দূরত্ব[i]
        • m_idx :=i
  • যদি m_idx -1 এর মত হয়, তাহলে
    • লুপ থেকে বেরিয়ে আসুন
  • c :=c + min_weight
  • itr[m_idx] :=সত্য
  • প্রতিটি জোড়ার জন্য i, j G[m_idx] এর মান, do
    • দূরত্ব[i] :=সর্বনিম্ন দূরত্ব[i], j
• রিটার্ন c

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def mst_find(G, s):দূরত্ব =[float("inf")] * len(G) দূরত্ব[s] =0 itr =[False] * len(G) c =0 যখন True:min_weight =float("inf") m_idx =-1 in range(len(G)):if itr[i] ==False:যদি দূরত্ব[i]  
ইনপুট
 
4, [(1, 2, 5), (1, 3, 5), (2, 3, 7), (1, 4, 4)], 3
 
আউটপুট
 
14