পাইথনে রঙিন শীর্ষবিন্দু নিয়মিত বহুভুজ থেকে সমদ্বিবাহু ত্রিভুজের সংখ্যা গণনা করার প্রোগ্রাম

ধরুন আমাদের একটি নিয়মিত বহুভুজ রয়েছে যার n বাহুগুলি n আকারের একটি বাইনারি স্ট্রিং হিসাবে উপস্থাপন করা হয়েছে। শীর্ষবিন্দুগুলি নীল (0) বা লাল (1) রঙে রঙিন হতে পারে। এগুলি ঘড়ির কাঁটার দিকে রঙিন হয় আমাদেরকে সমদ্বিবাহু ত্রিভুজের সংখ্যা গণনা করতে হবে যার শীর্ষবিন্দুগুলি নিয়মিত বহুভুজের শীর্ষবিন্দু এবং তাদের রঙ একই৷

সুতরাং, যদি ইনপুটটি বহুভুজের মত হয় ="111010", তাহলে আউটপুট হবে 2 কারণ

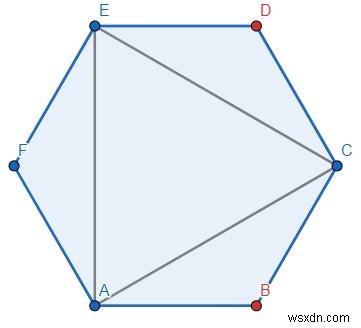
ACE এবং AFE দুটি ত্রিভুজ আছে।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি ফাংশন all() সংজ্ঞায়িত করুন। এটি n
যদি n mod 2 1 এর মত হয়, তাহলে, no :=n*(n-1) /2
অন্যথায়, না :=n*(n/2-1)
যদি n mod 3 0 এর মত হয়, তাহলে no :=no - n/3*2
রিটার্ন না
একটি ফাংশন non() সংজ্ঞায়িত করুন। এটি একটি, n
যদি n mod 2 1 এর মত হয়, তাহলে
- s0 :=0, s1 :=0
- i :=0
- যখন i
- যদি a[i] '0' এর মত হয়, তাহলে s0 :=s0 + 1
- অন্যথায় s1 :=s1 + 1
- i :=i + 1
s :=s0*s1*6
যদি n mod 3 0 এর মত হয়, তাহলে
- n1 :=n/3
- n2 :=n1*2
- i :=0
- যখন i
- যদি a[i] a[(i+n1)mod n] এর মত না হয়, তাহলে
  - s :=s - 2
- যদি a[i] a[(i+n2)mod n] এর মত না হয়, তাহলে
  - s :=s - 2
- i :=i + 1

অন্যথায়,

s00 :=0, s01 :=0, s10 :=0, s11 :=0, s :=0
i :=0
যখন i
যদি a[i] '0' এর মত হয়, তাহলে, s00 :=s00 + 1
অন্যথায় s01 :=s01 + 1
i :=i + 2

i :=1

যখন i

যদি a[i] '0' এর মত হয়, তাহলে, s10 :=s10 + 1

অন্যথায় s11 :=s11 + 1

i :=i + 2

s :=s + s00 * s01 * 8

s :=s + s10 * s11 * 8

s :=s + s00 * s11 * 4

s :=s + s10 * s01 * 4

n1 :=n/2

i :=0

যখন i

যদি a[i] a[(i + n1)mod n] এর মত না হয়, তাহলে

s :=s - 2

i :=i + 1

যদি n mod 3 0 এর মত হয়, তাহলে

n1 :=n/3
n2 :=n1*2
i :=0
যখন i
যদি a[i] a[(i+n1)mod n] এর মত না হয়, তাহলে
- s :=s - 2
যদি a[i] a[(i+n2)mod n] এর মত না হয়, তাহলে
- s :=s - 2
i :=i + 1

রিটার্ন s/2

প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -

n :=বহুভুজের আকার

না :=all(n) - non(polygon, n) /2

রিটার্ন না

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def all(n):
   if n % 2 == 1:
      no = n*(n-1)/2
   else:
      no = n*(n/2-1)
   if n % 3 == 0:
      no -= n/3*2
   return no

def non(a,n):
   if n % 2 == 1:
      s0 = s1 = 0
      i = 0
      while i < n:
         if a[i] == '0':
            s0 += 1
         else:
            s1 += 1
         i += 1
      s = s0*s1*6
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i<n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   else:
      s00 = s01 = s10 = s11 = s = 0
      i = 0
      while i <n:
         if a[i] == '0':
            s00 += 1
         else:
            s01 += 1
         i += 2
      i = 1
      while i < n:
         if a[i] == '0':
            s10 += 1
         else:
            s11 += 1
         i += 2
      s += s00 * s01 * 8
      s += s10 * s11 * 8
      s += s00 * s11 * 4
      s += s10 * s01 * 4
      n1 = n/2
      i = 0
      while i < n:
         if a[i] != a[int((i + n1)%n)]:
            s -= 2
         i += 1
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i < n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   return s/2

def solve(polygon):
   n = len(polygon)
   no = all(n) - non(polygon,n)/2
   return int(no)

polygon = "111010"
print(solve(polygon))

ইনপুট

1, 1000