ধরুন আমাদের এন বিভিন্ন নোড আছে। সব স্বতন্ত্র. বাইনারি সার্চ ট্রি গঠনের জন্য আমরা কতগুলো উপায়ে সেগুলো সাজাতে পারি তা আমাদের খুঁজে বের করতে হবে। বাইনারি সার্চ ট্রির জন্য আমরা জানি, বাম সাবট্রি সবসময় ছোট মান ধারণ করে এবং ডান সাবট্রি বৃহত্তর মান ধারণ করে।
এটি সমাধান করার জন্য, আমরা কাতালান সংখ্যা খুঁজে বের করব। কাতালান সংখ্যা C(n) n ভিন্ন কী সহ বাইনারি অনুসন্ধান গাছগুলিকে উপস্থাপন করে। সূত্রটি এরকম
$$C(n)=\frac{(2n)!}{(n+1)!\times n!}$$
সুতরাং, যদি ইনপুট n =3 এর মত হয়, তাহলে আউটপুট হবে 5 কারণ
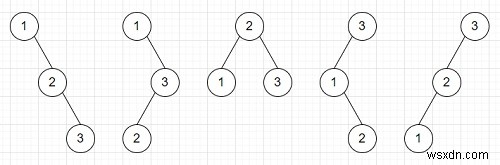
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- একটি ফাংশন ncr() সংজ্ঞায়িত করুন। এটি n, r লাগবে
- res :=1
- যদি r> n - r হয়, তাহলে
- r :=n - r
- আমি 0 থেকে r - 1 রেঞ্জের জন্য, কর
- res :=res *(n - i)
- res :=(res/(i + 1)) এর ফ্লোর
- রিটার্ন রিটার্ন
- মূল পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন
- c :=ncr(2 * n, n)
- c /(n + 1) এর রিটার্ন ফ্লোর
উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
<প্রে>ম্যাথ ইম্পোর্ট ফ্যাক্টোরিয়ালডেফ ncr(n, r) থেকে:res =1 যদি r> n - r:r =n - r i এর জন্য রেঞ্জ(r):res *=(n - i) res //=( i + 1) রিটার্ন resdef solve(n):c =ncr(2 * n, n) রিটার্ন c // (n + 1)n =3print(solve(n))ইনপুট
3
আউটপুট
5


