ধরুন আমাদের কাছে একটি নির্দেশিত গ্রাফের একটি প্রান্ত তালিকা রয়েছে, সেখানে n নোড রয়েছে এবং নোডের নামগুলি 0 থেকে n- 1। আমাদের দুটি পূর্ণসংখ্যার মানও রয়েছে a এবং b। আমাদের পরীক্ষা করতে হবে এমন কোনো নোড c আছে কি না যাতে আমরা c থেকে a এবং c থেকে b তে যেতে পারি।
সুতরাং, যদি ইনপুট মত হয়
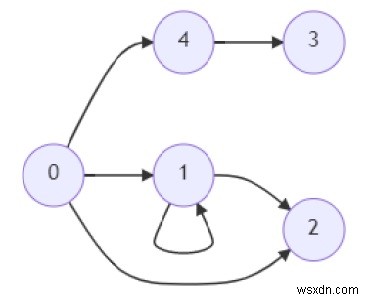
এবং a =2, b =3, তাহলে আউটপুট হবে True, কারণ এখানে c =0, তাই আমাদের কাছে 0 থেকে 2 এবং 0 থেকে 3 পর্যন্ত রুট রয়েছে।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- একটি ফাংশন DFS() সংজ্ঞায়িত করুন। এটি গ্রাফ, নোড, ভিজিট করা হবে
- যদি নোড পরিদর্শন না করা হয়, তাহলে
- নোডকে পরিদর্শন করা হিসাবে চিহ্নিত করুন
- গ্রাফ[নোড]-এ প্রতিটি x-এর জন্য, করুন
- DFS(গ্রাফ, x, পরিদর্শন করা)
- প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -
- গ্রাফ :=প্রান্ত_তালিকা থেকে সংলগ্নতা তালিকা তৈরি করুন
- পরিদর্শন_ক, পরিদর্শন_বি :=দুটি খালি সেট
- DFS(graph, a, visited_a)
- DFS(গ্রাফ, বি, পরিদর্শন করা_বি)
- উত্তর :=visited_b এবং visited_a এর সংযোগস্থল থেকে একটি নতুন তালিকা
- যদি উত্তর খালি না হয়, তাহলে
- সত্য ফেরান
- মিথ্যে ফেরত দিন
উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
def edge_list_to_graph(edges): s = set() for x, y in edges: s.add(x) s.add(y) s = len(list(s)) graph = [[] for x in range(s)] for x, y in edges: graph[y].append(x) return graph def DFS(graph, node, visited): if node not in visited: visited.add(node) for x in graph[node]: DFS(graph, x, visited) def solve(edges, a, b): graph = edge_list_to_graph(edges) visited_a, visited_b = set(), set() DFS(graph, a, visited_a) DFS(graph, b, visited_b) ans = list(visited_a.intersection(visited_b)) if ans: return True return False ed_list = [(0, 4),(4, 3),(1, 2),(0, 1),(0, 2),(1, 1)] a = 2 b = 3 print(solve(ed_list, a, b))
ইনপুট
[(0, 4),(4, 3),(1, 2),(0, 1),(0, 2),(1, 1)], 2, 3
আউটপুট
True


