আমাদেরকে একটি ধনাত্মক পূর্ণসংখ্যা n দেওয়া হয়েছে এবং শুধুমাত্র ঘড়ির কাঁটার দিকে O(1) অতিরিক্ত স্থান ব্যবহার করে n x n এর একটি সর্পিল ম্যাট্রিক্স তৈরি করা হয়েছে
স্পাইরাল ম্যাট্রিক্স হল একটি ম্যাট্রিক্স যা একটি স্পাইরালের মতো কাজ করে যা একটি বৃত্তের উৎপত্তি থেকে শুরু হবে এবং ঘড়ির কাঁটার দিকে ঘোরে। তাই কাজ হল 2 → 4 → 6 → 8 → 10 → 12 → 14 → 1 6→ 18 থেকে শুরু করে O(1) স্থান ব্যবহার করে সর্পিল আকারে ম্যাট্রিক্স মুদ্রণ করা।
নিচে স্পাইরাল ম্যাট্রিক্স -
এর উদাহরণ দেওয়া হল
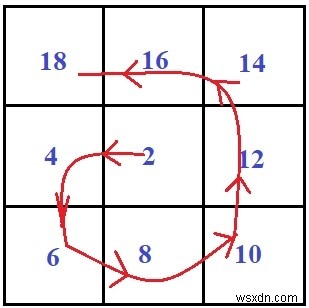
উদাহরণ
Input: 3 Output: 9 8 7 2 1 6 3 4 1
সীমাহীন স্থান দিয়ে কোডটি সমাধান করা সহজ হয়ে যায় তবে এটি সেরা প্রোগ্রাম হিসাবে দক্ষ নয় বা কোডটি এমন একটি যা মেমরি এবং সময় উভয় ক্ষেত্রেই দক্ষ। সুতরাং সর্পিল ক্রম বজায় রাখার জন্য চারটি লুপ ব্যবহার করা হয়, প্রতিটি ম্যাট্রিক্সের উপরের, ডান, নীচে এবং বাম কোণে কিন্তু যদি আমরা ম্যাট্রিক্সটিকে দুটি অংশে ভাগ করি অর্থাৎ উপরের ডান এবং নীচের বাম দিকে আমরা সরাসরি ধারণাটি ব্যবহার করতে পারি
উপরের ডান অর্ধেক জন্য,
mat[i][j] = (n-2*x)*(n-2*x)-(i-x)-(j-x)
নিচের বাম অর্ধেকের জন্য,
mat[i][j] = (n-2*x-2)*(n-2*x-2) + (i-x) + (j-x)
দ্রষ্টব্য -আমরা 2 এর ম্যাট্রিক্স মাল্টিপল প্রিন্ট করার জন্য প্রোগ্রাম লিখছি
অ্যালগরিদম
int spiralmatrix(int n) START STEP 1: DECLARE i, j, a, b, x STEP 2: LOOP FOR i = 0 AND i < n AND i++ LOOP FOR j = 0 AND j < n AND j++ FIND THE MINIMUM IN (i<j ) AND ASSIGN IT TO a FIND THE MINIMUM (n-1-i) < (n-1-j) AND ASSIGN IT TO b THEN ASSIGN THE LEAST VALUE FROM a AND b TO x IF i <= j THEN, PRINT THE VALUE OF 2* ((n-2*x)*(n-2*x) - (i-x) - (j-x)) ELSE PRINT THE VALUE OF 2*((n-2*x-2)*(n-2*x2) + (i-x) + (j-x)) END LOOP PRINT NEWLINE END LOOP STOP
উদাহরণ
#include <stdio.h>
//For n x n spiral matrix
int spiralmatrix(int n){
int i, j, a, b, x; // x stores the layer in which (i, j)th element exist
for ( i = 0; i < n; i++){
for ( j = 0; j < n; j++){
// Finds minimum of four inputs
a = ((i<j ? i : j));
b = ((n-1-i) < (n-1-j) ? (n-1-i) : (n-1-j));
x = a < b ? a : b;
// For upper right half
if (i <= j)
printf("%d\t ", 2 * ((n-2*x)*(n-2*x) - (i-x) - (j-x)));
// for lower left half
else
printf("%d\t ", 2*((n-2*x-2)*(n-2*x-2) + (i-x) + (j-x)));
}
printf("\n");
}
}
int main(int argc, char const *argv[]){
int n = 3;
spiralmatrix(n);
return 0;
} আউটপুট
যদি আমরা উপরের প্রোগ্রামটি চালাই তাহলে এটি নিম্নলিখিত আউটপুট −
তৈরি করবে18 16 14 4 2 12 6 8 10


