AVL ট্রি হল একটি স্ব-ভারসাম্যপূর্ণ বাইনারি সার্চ ট্রি যেখানে বাম এবং ডান সাবট্রির উচ্চতার মধ্যে পার্থক্য সমস্ত নোডের জন্য একের বেশি হতে পারে না
ট্রি ঘূর্ণন একটি অপারেশন যা একটি AVL গাছের উপাদানগুলির ক্রম হস্তক্ষেপ না করে গঠন পরিবর্তন করে। এটি গাছের একটি নোডকে উপরে এবং একটি নোডকে নিচে নিয়ে যায়। এটি গাছের আকৃতি পরিবর্তন করতে এবং ছোট সাবট্রিগুলিকে নীচে এবং বড় সাবট্রিগুলিকে উপরে সরানোর মাধ্যমে এর উচ্চতা হ্রাস করতে ব্যবহৃত হয়, যার ফলে অনেকগুলি গাছের ক্রিয়াকলাপের উন্নতি হয়। একটি ঘূর্ণনের দিক নির্ভর করে গাছের নোডগুলি কোন দিকে স্থানান্তরিত হয় যখন অন্যরা বলে যে এটি নির্ভর করে কোন শিশুটি মূলের স্থান নেয় তার উপর। এটি AVL Tree বাস্তবায়নের জন্য একটি C++ প্রোগ্রাম।
ফাংশন বর্ণনা:
উচ্চতা(avl *) :এটি প্রদত্ত AVL গাছের উচ্চতা গণনা করে।
পার্থক্য(avl *) :এটি প্রদত্ত গাছের উপবৃক্ষের উচ্চতার মধ্যে পার্থক্য গণনা করে
avl *rr_rotat(avl *) :ডান-ডান ঘূর্ণন হল ডান ঘূর্ণনের পরে ডান ঘূর্ণনের সংমিশ্রণ।
avl *ll_rotat(avl *) :একটি বাম-বাম ঘূর্ণন বাম ঘূর্ণন দ্বারা অনুসরণ করা বাম ঘূর্ণনের সংমিশ্রণ।
avl *lr_rotat(avl*) :একটি বাম-ডান ঘূর্ণন হল বাম ঘূর্ণনের একটি সংমিশ্রণ যার পরে ডান ঘূর্ণন।
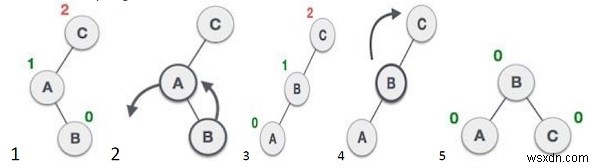
avl *rl_rotat(avl *) :এটি ডান ঘূর্ণনের একটি সংমিশ্রণ যার পরে বাম ঘূর্ণন।
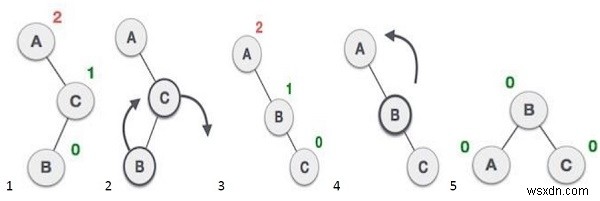
avl * ব্যালেন্স(avl *): এটি ব্যালেন্স ফ্যাক্টর পেয়ে গাছের ভারসাম্য ক্রিয়া সম্পাদন করে
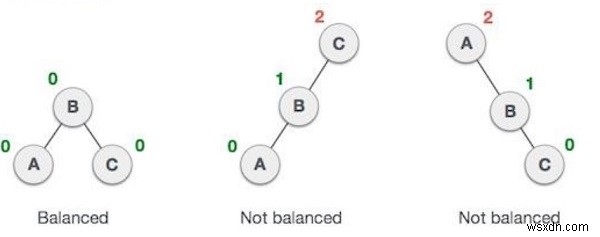
avl * insert(avl*, int) :এটা সন্নিবেশ অপারেশন সঞ্চালন. এই ফাংশন ব্যবহার করে ট্রিতে মান সন্নিবেশ করান।
শো(avl*, int) :এটি গাছের মান প্রদর্শন করে।
inorder(avl *) :একটি ক্রমানুসারে একটি গাছ অতিক্রম করে৷
প্রি-অর্ডার(avl *) :একটি প্রি-অর্ডার পদ্ধতিতে একটি গাছ অতিক্রম করে৷
পোস্টরডার(avl*) :পোস্ট-অর্ডার পদ্ধতিতে একটি গাছ অতিক্রম করে।
উদাহরণ
#include<iostream>
#include<cstdio>
#include<sstream>
#include<algorithm>
#define pow2(n) (1 << (n))
using namespace std;
struct avl {
int d;
struct avl *l;
struct avl *r;
}*r;
class avl_tree {
public:
int height(avl *);
int difference(avl *);
avl *rr_rotat(avl *);
avl *ll_rotat(avl *);
avl *lr_rotat(avl*);
avl *rl_rotat(avl *);
avl * balance(avl *);
avl * insert(avl*, int);
void show(avl*, int);
void inorder(avl *);
void preorder(avl *);
void postorder(avl*);
avl_tree() {
r = NULL;
}
};
int avl_tree::height(avl *t) {
int h = 0;
if (t != NULL) {
int l_height = height(t->l);
int r_height = height(t->r);
int max_height = max(l_height, r_height);
h = max_height + 1;
}
return h;
}
int avl_tree::difference(avl *t) {
int l_height = height(t->l);
int r_height = height(t->r);
int b_factor = l_height - r_height;
return b_factor;
}
avl *avl_tree::rr_rotat(avl *parent) {
avl *t;
t = parent->r;
parent->r = t->l;
t->l = parent;
cout<<"Right-Right Rotation";
return t;
}
avl *avl_tree::ll_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = t->r;
t->r = parent;
cout<<"Left-Left Rotation";
return t;
}
avl *avl_tree::lr_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = rr_rotat(t);
cout<<"Left-Right Rotation";
return ll_rotat(parent);
}
avl *avl_tree::rl_rotat(avl *parent) {
avl *t;
t= parent->r;
parent->r = ll_rotat(t);
cout<<"Right-Left Rotation";
return rr_rotat(parent);
}
avl *avl_tree::balance(avl *t) {
int bal_factor = difference(t);
if (bal_factor > 1) {
if (difference(t->l) > 0)
t = ll_rotat(t);
else
t = lr_rotat(t);
}
else if (bal_factor < -1) {
if (difference(t->r) > 0)
t= rl_rotat(t);
else
t = rr_rotat(t);
}
return t;
}
avl *avl_tree::insert(avl *r, int v) {
if (r == NULL) {
r= new avl;
r->d = v;
r->l = NULL;
r->r= NULL;
return r;
}
else if (v< r->d) {
r->l= insert(r->l, v);
r = balance(r);
}
else if (v >= r->d) {
r->r= insert(r->r, v);
r = balance(r);
}
return r;
}
void avl_tree::show(avl *p, int l) {
int i;
if (p != NULL) {
show(p->r, l+ 1);
cout<<" ";
if (p == r)
cout << "Root -> ";
for (i = 0; i < l&& p != r; i++)
cout << " ";
cout << p->d;
show(p->l, l + 1);
}
}
void avl_tree::inorder(avl *t) {
if (t == NULL)
return;
inorder(t->l);
cout << t->d << " ";
inorder(t->r);
}
void avl_tree::preorder(avl *t) {
if (t == NULL)
return;
cout << t->d << " ";
preorder(t->l);
preorder(t->r);
}
void avl_tree::postorder(avl *t) {
if (t == NULL)
return;
postorder(t ->l);
postorder(t ->r);
cout << t->d << " ";
}
int main() {
int c, i;
avl_tree avl;
while (1) {
cout << "1.Insert Element into the tree" << endl;
cout << "2.show Balanced AVL Tree" << endl;
cout << "3.InOrder traversal" << endl;
cout << "4.PreOrder traversal" << endl;
cout << "5.PostOrder traversal" << endl;
cout << "6.Exit" << endl;
cout << "Enter your Choice: ";
cin >> c;
switch (c) {
case 1:
cout << "Enter value to be inserted: ";
cin >> i;
r= avl.insert(r, i);
break;
case 2:
if (r == NULL) {
cout << "Tree is Empty" << endl;
continue;
}
cout << "Balanced AVL Tree:" << endl;
avl.show(r, 1);
cout<<endl;
break;
case 3:
cout << "Inorder Traversal:" << endl;
avl.inorder(r);
cout << endl;
break;
case 4:
cout << "Preorder Traversal:" << endl;
avl.preorder(r);
cout << endl;
break;
case 5:
cout << "Postorder Traversal:" << endl;
avl.postorder(r);
cout << endl;
break;
case 6:
exit(1);
break;
default:
cout << "Wrong Choice" << endl;
}
}
return 0;
} আউটপুট
1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 13 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 15 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 5 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 11 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 4 Left-Left Rotation1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 8 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 3 Inorder Traversal: 4 5 8 10 11 13 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 4 Preorder Traversal: 10 5 4 8 13 11 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 5 Postorder Traversal: 4 8 5 11 16 15 13 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 14 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 3 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 7 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 9 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 52 Right-Right Rotation 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 6


