বেলম্যান ফোর্ড অ্যালগরিদম হল ডায়নামিক প্রোগ্রামিং অ্যালগরিদম যা প্রারম্ভিক শীর্ষ হিসাবে বিবেচিত একটি শীর্ষ থেকে গণনা করা যে কোনও শীর্ষের সংক্ষিপ্ততম পথ খুঁজে পেতে ব্যবহৃত হয়। এই অ্যালগরিদম পুনরাবৃত্তিমূলক পদ্ধতি অনুসরণ করে এবং ক্রমাগত সংক্ষিপ্ততম পথ খুঁজে বের করার চেষ্টা করে। ওজনযুক্ত গ্রাফে বেলম্যান ফোর্ড অ্যালগরিদম।
এই অ্যালগরিদমটি 1955 সালে আলফোনসো শিম্বেল দ্বারা প্রস্তাবিত হয়েছিল৷ অ্যালগরিদমটিতে রিচার্ড বেলম্যান এবং লেস্টার ফোর্ড দ্বারা সংশোধন করা হয়েছে 1956 এবং 1958 সালে, এই অ্যালগরিদমটির কারণে নামকরণ করা হয়েছিল বেলম্যান ফোর্ড অ্যালগরিদম . এই অ্যালগরিদমটিও 1957 সালে এওয়ার্ড এফ. মুর দ্বারা সংশোধিত হয়েছিল, যা এটির নামকরণ করেছে বেলম্যান-ফোর্ড-মুর অ্যালগরিদম .
এই অ্যালগরিদমটি আরও ভাল কারণ এটি নেতিবাচক ওজনের সাথে প্রান্তগুলি পরিচালনা করতে পারে। যদিও অ্যালগরিদমটি ডিজকস্ট্রার অ্যালগরিদমের চেয়ে ধীর, তবে এটি একটি ভাল কারণ এটি আরও বহুমুখী ধরণের গ্রাফ পরিচালনা করে৷
অ্যালগরিদম
Input : weighted graph and starting vertex Output : shortest distance between all vertices from the src. For negative weight cycle, the same will be returned as the weight cannot be calculated.
অ্যালগরিদম
Step 1 : This is the initialisation step, an array is created that stores the distance of all vertices from the initial vertex. The array say dist[] of size equal to the number of vertices in the graph. Step 2 : Calculate the shortest distance of vertex. Loop through step 3 for n-1 number of times ( n is the number of vertices of graph). Step 3 : Follow following steps for each edge i-j Step 3.1 : If dist[v] > dist[u] + weight[uv]. Then, dist[v] = dist[u] + weight[uv]. Step 4 : Check and flag if there is any negative cycle. If step 3.1 executes then there is a negative cycle.
নেতিবাচক চক্র :যদি নিয়মিত প্রান্ত ট্রাভার্সালের চেয়ে ছোট পথ থাকে তবে একটি নেতিবাচক চক্র রয়েছে।
উদাহরণ
আসুন কিছু গ্রাফ সম্পর্কিত সমস্যার সমাধান করে অ্যালগরিদম সম্পর্কে আরও শিখি।
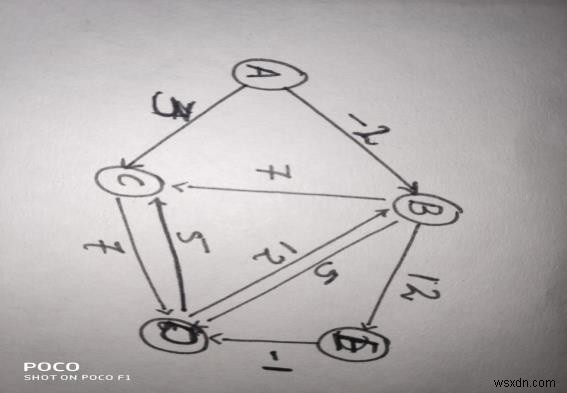
আপনি গ্রাফের সমস্ত শিরোনাম এবং প্রান্তগুলি তাদের সাথে সম্পর্কিত ওজন সহ দেখতে পারেন৷
চলুন শীর্ষ A এবং শীর্ষবিন্দু E এর মধ্যে সবচেয়ে কম দূরত্ব খুঁজে বের করা যাক বেলম্যান-ফোর্ড অ্যালগরিদম ব্যবহার করে৷
উৎস শীর্ষবিন্দু (A) শূন্য 0 এ সেট করুন এবং বাকি দূরত্বগুলি অসীম ∞ এ সেট করুন।
A B C D E 0 ∞ ∞ ∞ ∞
প্রান্তের ওজন পরীক্ষা করা হচ্ছে A-B এবং তারপর A-C ,
A- B-এর জন্য আমাদের একটি মাত্র পথ আছে কিন্তু A-C-এর জন্য, আমাদের দুটি পথ আছে যেগুলো অতিক্রম করা যায় এবং আমরা পরীক্ষা করব কোনটি সবচেয়ে ছোট।
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ - for (A-B) 0 -2 3 ∞ ∞ - for (A-C)
শীর্ষবিন্দুর পরের জন্য, আমরা গণনা করব এবং প্রাথমিক শীর্ষবিন্দুর জন্য সবচেয়ে ছোট দূরত্ব।
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ 0 -2 3 3 10
অ্যালগরিদম ব্যবহার করে সর্বনিম্ন দূরত্ব হল 10। পথ অতিক্রম করা A-B-E . এটি ব্যবহার করে আমরা আরও দেখতে পেলাম যে একটি নেতিবাচক চক্র রয়েছে।
উদাহরণ
#include <bits/stdc++.h>
struct Edge {
int src, dest, weight;
};
struct Graph {
int V, E;
struct Edge* edge;
};
struct Graph* createGraph(int V, int E) {
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
void BellmanFord(struct Graph* graph, int src) {
int V = graph->V;
int E = graph->E;
int dist[V];
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v]) {
printf("Graph contains negative weight cycle");
return;
}
}
printf("Vertex :\t\t\t ");
for (int i = 0; i < V; ++i)
printf("%d \t", i);
printf("\nDistance From Source : ");
for (int i = 0; i < V; ++i)
printf("%d \t",dist[i]);
return;
}
int main() {
int V = 5;
int E = 8;
struct Graph* graph = createGraph(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;
BellmanFord(graph, 0);
return 0;
} আউটপুট
Vertex : 0 1 2 3 4 Distance From Source : 0 -1 2 -2 1


