বাইনারী সার্চ ট্রি (BST) একটি বিশেষ ধরনের গাছ যা নিম্নলিখিত নিয়মগুলি অনুসরণ করে -
- বাম চাইল্ড নোডের মান সবসময়ই প্যারেন্ট নোটের চেয়ে কম হয়
- অভিভাবক নোডের চেয়ে ডান চাইল্ড নোডের মূল্য বেশি।
- সমস্ত নোড পৃথকভাবে একটি বাইনারি অনুসন্ধান গাছ গঠন করে।
বাইনারি সার্চ ট্রি (BST) -
এর উদাহরণ

সার্চ, ন্যূনতম এবং সর্বোচ্চ সন্ধানের মতো ক্রিয়াকলাপের জটিলতা কমাতে একটি বাইনারি অনুসন্ধান ট্রি তৈরি করা হয়েছে৷
বিএসটি-তে সার্চ অপারেশন
একটি বাইনারি অনুসন্ধান গাছে একটি অনুসন্ধান সম্পাদন করা,
আমাদের গাছে একটি চাবি অনুসন্ধান করতে হবে। এর জন্য, আমরা কীটিকে গাছের রুট নোডের সাথে তুলনা করব।
যদি কী রুট নোডের সমান হয়, কী পাওয়া যায়।
যদি কীটির মান রুট নোডের চেয়ে বেশি হয়, তাহলে সঠিক সাবট্রি নিন এবং কীটি অনুসন্ধান করুন৷
যদি কীটির মান রুট নোডের চেয়ে কম হয়, বাম সাবট্রি নিন এবং কীটি অনুসন্ধান করুন৷
উদাহরণ
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void traversetree(struct node *root){
if (root != NULL){
traversetree(root->left);
printf("%d \t", root->key);
traversetree(root->right);
}
}
struct node* search(struct node* root, int key){
if (root == NULL || root->key == key)
return root;
if (root->key < key)
return search(root->right, key);
return search(root->left, key);
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 23);
insert(root, 15);
insert(root, 12);
insert(root, 17);
insert(root, 32);
insert(root, 29);
insert(root, 45);
printf("The tree is :\n");
traversetree(root);
printf("\nSearching for 12 in this tree ");
if(search(root , 12))
printf("\nelement found");
else
printf("\nelement not found");
return 0;
} আউটপুট
The tree is : 12 15 17 23 29 32 45 Searching for 12 in this tree element found
বিএসটি-তে সন্নিবেশ অপারেশন
একটি বিএসটি-তে সন্নিবেশ অপারেশনটি সন্নিবেশের জন্য গাছের পাতার নোডে সঞ্চালিত হয় আমরা রুট নোডের সাথে নোডের তুলনা শুরু করব এবং নোডের সঠিক অবস্থান খুঁজে বের করব এবং তারপরে এটি স্থাপন করব। নিম্নলিখিত উদাহরণটি আপনার কাছে এটিকে আরও স্পষ্ট করবে৷

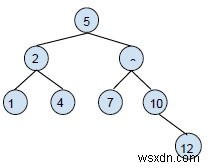
এই BST-তে 12 ঢোকানো হচ্ছে।
আমরা 12 কে রুট নোড 12> 5 এর সাথে তুলনা করব, এটি সঠিক সাবট্রির অন্তর্গত।
12 কে ডান চাইল্ড নোড 12> 8 এর সাথে তুলনা করুন, এটি ডান সাব চাইল্ডের ডানের অন্তর্গত।
ডান সাবট্রি 12>10 এর ডান সাব চাইল্ডের সাথে 12 টির তুলনা করুন, এর অবস্থান এই নোডের ডানদিকে৷
গঠিত নতুন গাছ হবে,
উদাহরণ
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void traversetree(struct node *root){
if (root != NULL){
traversetree(root->left);
printf("%d \t", root->key);
traversetree(root->right);
}
}
struct node* insert(struct node* node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 23);
insert(root, 15);
insert(root, 12);
insert(root, 17);
insert(root, 32);
insert(root, 29);
printf("The tree is :\n");
traversetree(root);
printf("\nInseting 45 to the tree\n");
insert(root, 45);
printf("Tree after insertion is :\n");
traversetree(root);
return 0;
} আউটপুট
The tree is : 12 15 17 23 29 32 Inserting 45 to the tree Tree after insertion is : 12 15 17 23 29 32 45


