ধরুন আমাদের একটি কোম্পানীর এন কর্মচারী রয়েছে যার প্রতিটি কর্মচারীর জন্য একটি অনন্য আইডি রয়েছে। এই আইডিগুলি 0 থেকে n - 1 এর মধ্যে রয়েছে৷ কোম্পানির প্রধানের কাছে হেডআইডি রয়েছে৷ ম্যানেজার অ্যারেতে প্রত্যেক কর্মচারীর একজন সরাসরি ম্যানেজার থাকে যেখানে ম্যানেজার[i] হল i-th কর্মচারীর সরাসরি ম্যানেজার, ম্যানেজার[headID] =-1। এছাড়াও এটি নিশ্চিত যে অধস্তন সম্পর্কগুলির একটি গাছের মতো কাঠামো রয়েছে। এখানে কোম্পানির প্রধান একটি জরুরি খবর কোম্পানির সমস্ত কর্মচারীদের জানাতে চান। তিনি তার সরাসরি অধস্তনদের অবহিত করতে পারেন এবং তারা তাদের অধস্তনদের অবহিত করবে এবং তাই যতক্ষণ না সমস্ত কর্মচারী জরুরী খবর সম্পর্কে জানতে পারে। i-th কর্মচারীর তার সমস্ত সরাসরি অধস্তনদের অবহিত করার জন্য informTime[i] মিনিটের প্রয়োজন (তাই informTime[i] মিনিটের পরে, তার সমস্ত সরাসরি অধস্তনরা খবর ছড়াতে শুরু করতে পারে)। জরুরী সংবাদ সম্পর্কে সমস্ত কর্মচারীকে জানানোর জন্য আমাদের প্রয়োজনীয় মিনিটের সংখ্যা খুঁজে বের করতে হবে। সুতরাং ইনপুট যদি হয় n =6, headID =2, ম্যানেজার =[2,2,-1,2,2,2], infromTime =[0,0,1,0,0,0], তাহলে আউটপুট 1 হবে।
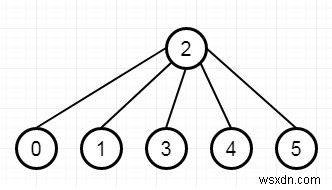
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
ret :=0
-
n আকারের গ্রাফ নামে একটি অ্যারে সংজ্ঞায়িত করুন, রুট সেট করুন :=-1
-
আমি পরিসীমা 0 থেকে ম্যানেজার অ্যারের আকারের জন্য
-
u :=ব্যবস্থাপনা[i] এবং v :=i
-
যদি u-1 হয়, তাহলে root :=v সেট করুন এবং পরবর্তী পুনরাবৃত্তির জন্য যান
-
গ্রাফ[u]
-এ v সন্নিবেশ করান
-
-
একটি সারি q সংজ্ঞায়িত করুন, q এর মধ্যে রুট সন্নিবেশ করুন এবং n আকারের সময় নামক একটি অ্যারে সংজ্ঞায়িত করুন
-
যতক্ষণ না q খালি না হয়
-
curr :=q এর ফ্রন্ট এলিমেন্ট, এবং q থেকে ফ্রন্ট এলিমেন্ট মুছে দিন
-
যদি গ্রাফ[curr] এর তালিকার আকার 0 হয়, তাহলে পরবর্তী পুনরাবৃত্তিতে চলে যান
-
গ্রাফ[curr]
-এর তালিকার আকার 0 থেকে সীমার মধ্যে-
q
-এ গ্রাফ[curr, i] সন্নিবেশ করান -
সময়[গ্রাফ[curr, i]] :=time[curr] + informTime[curr]
-
-
-
0 থেকে n – 1 রেঞ্জের i জন্য:ret :=ret এবং সময়ের সর্বোচ্চ[i]
-
রিটার্ন রিটার্ন
উদাহরণ (C++)
আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
int ret = 0;
vector <int> graph[n];
int root = -1;
for(int i = 0; i < manager.size(); i++){
int u = manager[i];
int v = i;
if(u == -1) {
root = v;
continue;
}
graph[u].push_back(v);
}
queue <int> q;
q.push(root);
vector <int> time(n);
while(!q.empty()){
int curr = q.front();
q.pop();
if(!graph[curr].size()) continue;
for(int i = 0; i < graph[curr].size(); i++){
q.push(graph[curr][i]);
time[graph[curr][i]] = time[curr] + informTime[curr];
}
}
for(int i = 0; i <n; i++)ret = max(ret, time[i]);
return ret;
}
};
main(){
vector<int> v = {2,2,-1,2,2,2}, v1 = {0,0,1,0,0,0};
Solution ob;
cout << (ob.numOfMinutes(6, 2, v, v1));
} ইনপুট
6 2 [2,2,-1,2,2,2] [0,0,1,0,0,0]
আউটপুট
1


