এই সমস্যায়, আমাদের একটি বাইনারি গাছ দেওয়া হয়। আমাদের কাজ হল রিকারশন এবং স্ট্যাক ছাড়াই ব্যবহার না করে বাইনারি ট্রির পোস্টঅর্ডার ট্রাভার্সাল প্রিন্ট করা .
বাইনারী গাছ একটি বিশেষ ধরনের গাছ যাতে প্রতিটি নোডে সর্বোচ্চ 2টি চাইল্ড নোড থাকতে পারে৷
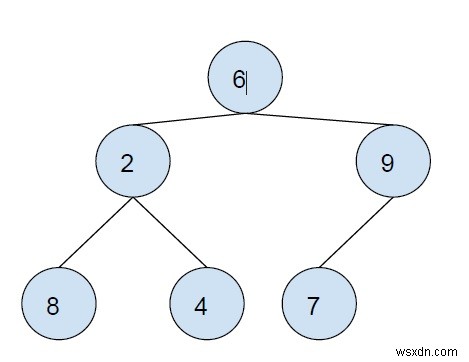
পোস্টডার ট্রাভার্সাল একটি ট্রি ট্রাভার্সাল টেকনিক, যেখানে প্রথম বাম সাবট্রিটি ডান সাবট্রির চেয়ে এবং মূলটি শেষে ট্রাভার্স করা হয়।
উপরের গাছের পোস্টরডার ট্রাভার্সাল - 8 4 2 7 9 6
পুনরাবৃত্ত এবং স্ট্যাক ব্যবহার না করে গাছটি অতিক্রম করতে। আমরা গভীরতা-প্রথম অনুসন্ধান ভিত্তিক কৌশল করব এবং ডেটা একটি হ্যাশ টেবিলে সংরক্ষণ করা হবে .
উদাহরণ
এই সমাধানের বাস্তবায়ন দেখানোর জন্য প্রোগ্রাম,
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
void postOrderTraversal(struct Node* head) {
struct Node* temp = head;
unordered_set<Node*> visited;
while (temp && visited.find(temp) == visited.end()) {
if (temp->left &&
visited.find(temp->left) == visited.end())
temp = temp->left;
else if (temp->right &&
visited.find(temp->right) == visited.end())
temp = temp->right;
else {
cout<<temp->data<<"\t";
visited.insert(temp);
temp = head;
}
}
}
struct Node* insertNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main(){
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
} আউটপুট
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6
একই সমাধান আপডেট করা যেতে পারে এবং হ্যাশ টেবিলের ব্যবহার বাদ দেওয়া যেতে পারে। যেহেতু এর কাজ হল পরিদর্শন করা নোডগুলি সংরক্ষণ করা। সিস্টেমের উপর লোড কমাতে আমরা প্রতিটি নোডে একটি পরিদর্শন করা পতাকা যোগ করব এটি নিজেই গাছ, এটি আমাদের অ্যালগরিদমকে আরও ভাল করে তুলবে৷
একটি আরও কার্যকর সমাধান হল একটি ক্রমহীন মানচিত্র ব্যবহার করা, এটি ট্র্যাকব্যাকের ওভারহেডকে মাথার দিকে কমিয়ে দেবে৷
উদাহরণ
বাস্তবায়ন দেখানোর জন্য প্রোগ্রাম
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
bool visited;
};
void postOrderTraversal(Node* root) {
Node* n = root;
unordered_map<Node*, Node*> postorder;
postorder.insert(pair<Node*, Node*>(root, nullptr));
while (n) {
if (n->left && postorder.find(n->left) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->left, n));
n = n->left;
}
else if (n->right && postorder.find(n->right) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->right, n));
n = n->right;
}
else {
cout<<n->data<<"\t";
n = (postorder.find(n))->second;
}
}
}
struct Node* insertNode(int data) {
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
node->visited = false;
return (node);
}
int main() {
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
} আউটপুট
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6


