C++ এ একটি নেটওয়ার্কে জটিল সংযোগ

ধরুন n সার্ভার আছে। এবং এগুলিকে 0 থেকে n-1 পর্যন্ত নম্বর দেওয়া হয়েছে একটি অনির্দেশিত সার্ভার-টু-সার্ভার সংযোগ দ্বারা সংযুক্ত একটি নেটওয়ার্ক তৈরি করে যেখানে সংযোগগুলি [i] =[a,b] সার্ভার a এবং b এর মধ্যে একটি সংযোগ উপস্থাপন করে। সমস্ত সার্ভার সরাসরি বা অন্য কিছু সার্ভারের মাধ্যমে সংযুক্ত। এখন, একটি সমালোচনামূলক সংযোগ একটি সংযোগ যা, যদি এটি সরানো হয়, এটি কিছু সার্ভারকে অন্য কোনো সার্ভারে পৌঁছাতে অক্ষম করে তুলবে। আমাদের সমস্ত সমালোচনামূলক সংযোগ খুঁজে বের করতে হবে।

সুতরাং, যদি ইনপুট হয় n =4 এবং সংযোগ =[[0,1],[1,2],[2,0],[1,3]],

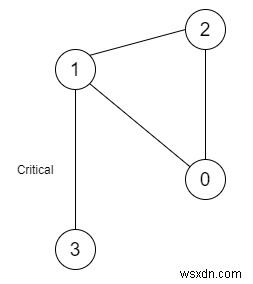
তাহলে আউটপুট হবে [[1,3]]

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি সেট সংজ্ঞায়িত করুন

• একটি অ্যারে ডিস্ক সংজ্ঞায়িত করুন

• একটি অ্যারে কম সংজ্ঞায়িত করুন

• একটি 2D অ্যারে ret সংজ্ঞায়িত করুন

• একটি ফাংশন dfs(), এটি নোড, par, একটি 2D অ্যারে গ্রাফ গ্রহণ করবে,

• যদি নোড পরিদর্শন করা হয়, তাহলে -

  • ফেরত

• ভিজিটেড

  -এ নোড সন্নিবেশ করান

• ডিস্ক [নোড] :=সময়

• কম [নোড] :=সময়

• (1 দ্বারা সময় বাড়ান)

• গ্রাফ[নোড]

  -এ সমস্ত উপাদান x এর জন্য

  • যদি x সমান হয়, তাহলে −

    • নিম্নলিখিত অংশ উপেক্ষা করুন, পরবর্তী পুনরাবৃত্তি এড়িয়ে যান

  • যদি x পরিদর্শনে না থাকে, তাহলে −

    • dfs(x, নোড, গ্রাফ)

    • low[নোড] :=সর্বনিম্ন নিম্ন [নোড] এবং নিম্ন [x]

    • যদি ডিস্ক[নোড]

      • ret

        শেষে { node, x } সন্নিবেশ করুন

  • অন্যথায়

    • low[নোড] :=সর্বনিম্ন কম [নোড] এবং ডিস্ক[x]

• প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন -

  • ডিস্কের আকার n + 1

    হিসাবে সেট করুন

  • n + 1

    হিসাবে কম আকার সেট করুন

  • সময় :=0

  • আকার গ্রাফ n + 1

    এর তালিকার একটি বিন্যাস সংজ্ঞায়িত করুন

  • আরম্ভ করার জন্য i :=0, যখন i

    • u :=v[i, 0]

    • w :=v[i, 1]

    • গ্রাফ[u]

      এর শেষে w সন্নিবেশ করুন

    • গ্রাফের শেষে u ঢোকান[w]

  • dfs(0, -1, গ্রাফ)

  • রিটার্ন রিটার্ন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

#include <bits/stdc++.h>
using namespace std;
void print_vector(vector<vector<auto> > v){
   cout << "[";
   for(int i = 0; i<v.size(); i++){
      cout << "[";
      for(int j = 0; j <v[i].size(); j++){
         cout << v[i][j] << ", ";
      }
      cout << "],";
   }
   cout << "]"<<endl;
}
class Solution {
   public:
   set<int> visited;
   vector<int> disc;
   vector<int> low;
   int time;
   vector<vector<int> > ret;
   void dfs(int node, int par, vector<int> graph[]) {
      if (visited.count(node))
      return;
      visited.insert(node);
      disc[node] = low[node] = time;
      time++;
      for (int x : graph[node]) {
         if (x == par)
         continue;
         if (!visited.count(x)) {
            dfs(x, node, graph);
            low[node] = min(low[node], low[x]);
            if (disc[node] < low[x]) {
               ret.push_back({ node, x });
            }
         } else{
            low[node] = min(low[node], disc[x]);
         }
      }
   }
   vector<vector<int> > criticalConnections(int n, vector<vector<int> >& v) {
      disc.resize(n + 1);
      low.resize(n + 1);
      time = 0;
      vector<int> graph[n + 1];
      for (int i = 0; i < v.size(); i++) {
         int u = v[i][0];
         int w = v[i][1];
         graph[u].push_back(w);
         graph[w].push_back(u);
      }
      dfs(0, -1, graph);
      return ret;
   }
};
main(){
   Solution ob;
   vector<vector<int>> v = {{0,1},{1,2},{2,0},{1,3}};
   print_vector(ob.criticalConnections(4,v));
}

ইনপুট

4, {{0,1},{1,2},{2,0},{1,3}}

আউটপুট

[[1, 3, ],]