ধরুন আমাদের কাছে (অক্ষ-সারিবদ্ধ) আয়তক্ষেত্রগুলির একটি তালিকা রয়েছে। এখানে প্রতিটি আয়তক্ষেত্র [i] ={x1, y1, x2, y2}, যেখানে (x1, y1) হল নীচে-বাম কোণের বিন্দু এবং (x2, y2) হল উপরের-ডানদিকের কোণের বিন্দু। ith আয়তক্ষেত্র।
আমাদের সমতলের সমস্ত আয়তক্ষেত্র দ্বারা আচ্ছাদিত মোট এলাকা খুঁজে বের করতে হবে। উত্তরটি খুব হতে পারে, তাই আমরা মডুলো 10^9 + 7 ব্যবহার করতে পারি।
সুতরাং, যদি ইনপুট মত হয়
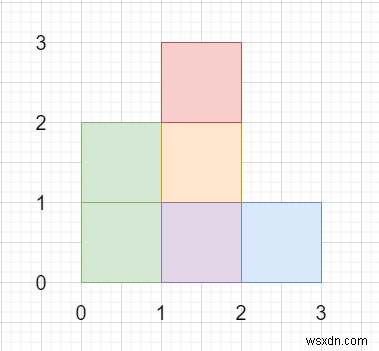
তাহলে আউটপুট হবে 6।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
m =10^9 + 7
-
একটি ফাংশন add() সংজ্ঞায়িত করুন, এটি a, b,
লাগবে -
ফিরুন ((a mod m) + (b mod m) mod m)
-
একটি ফাংশন কম্প্রেস সংজ্ঞায়িত করুন এটি 2d ম্যাট্রিক্স v
নেবে -
একটি অ্যারের তাপমাত্রা সংজ্ঞায়িত করুন
-
আরম্ভ করার জন্য i :=0, যখন i
-
টেম্পের শেষে v[i, 0] ঢোকান
-
টেম্পের শেষে v[i, 2] ঢোকান
-
-
অ্যারের তাপমাত্রা সাজান
-
একটি মানচিত্র সংজ্ঞায়িত করুন, আবার
-
idx :=0
-
আরম্ভ করার জন্য i :=0, যখন i
-
যদি temp[i] ret-এর সদস্য না হয়, তাহলে −
-
ret[temp[i]] :=idx
-
(আইডিএক্স 1 দ্বারা বাড়ান)
-
-
-
রিটার্ন রিটার্ন
-
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
-
একটি অ্যারে xv
সংজ্ঞায়িত করুন -
xv
এর শেষে { 0 } ঢোকান -
আরম্ভ করার জন্য i :=0, যখন i
-
xv
এর শেষে v[i, 0] ঢোকান -
xv
এর শেষে v[i, 2] ঢোকান
-
-
অ্যারে xv
সাজান -
uniItr =xv
এর অনন্য উপাদান সহ একটি তালিকার প্রথম উপাদান -
uniItr মুছুন, xv
থেকে -
একটি মানচিত্র সূচক সংজ্ঞায়িত করুন
-
idx :=0
-
আরম্ভ করার জন্য i :=0, যখন i
-
index[xv[i]] :=i
-
-
সূচক আকারের সমান আকারের একটি অ্যারে গণনা সংজ্ঞায়িত করুন
-
একটি 2D অ্যারে x
সংজ্ঞায়িত করুন -
আরম্ভ করার জন্য i :=0, যখন i
-
x1 :=v[i, 0], y1 :=v[i, 1]
-
x2 :=v[i, 2], y2 :=v[i, 3]
-
x
এর শেষে { y1, x1, x2, 1 } ঢোকান -
x
এর শেষে { y2, x1, x2, -1 } ঢোকান
-
-
অ্যারে x
সাজান -
ret :=0
-
যোগফল :=0, বর্তমানY :=0
-
আরম্ভ করার জন্য i :=0, যখন i
-
y :=x[i, 0]
-
x1 :=x[i, 1], x2 :=x[i, 2]
-
sig :=x[i, 3]
-
ret :=add(ret, (y - currentY) * যোগফল)
-
currentY :=y
-
আরম্ভ করার জন্য i :=index[x1], যখন i
-
count[i] :=count[i] + sig
-
-
যোগফল :=0
-
আরম্ভ করার জন্য i :=0, যখন i <গণনার আকার, আপডেট (i 1 দ্বারা বৃদ্ধি), −
-
যদি গণনা [i]> 0 হয়, তাহলে
-
যোগফল :=যোগফল + (xv[i + 1] - xv[i])
-
-
-
-
রিটার্ন ret mod m
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
typedef long long int lli;
const int m = 1e9 + 7;
class Solution {
public:
lli add(lli a, lli b){
return ((a % m) + (b % m) % m);
}
map<int, int> compress(vector<vector<int> >& v){
vector<int> temp;
for (int i = 0; i < v.size(); i++) {
temp.push_back(v[i][0]);
temp.push_back(v[i][2]);
}
sort(temp.begin(), temp.end());
map<int, int> ret;
int idx = 0;
for (int i = 0; i < temp.size(); i++) {
if (!ret.count(temp[i])) {
ret[temp[i]] = idx;
idx++;
}
}
return ret;
}
int rectangleArea(vector<vector<int> >& v){
vector<int> xv;
xv.push_back({ 0 });
for (int i = 0; i < v.size(); i++) {
xv.push_back(v[i][0]);
xv.push_back(v[i][2]);
}
sort(xv.begin(), xv.end());
vector<int>::iterator uniItr = unique(xv.begin(), xv.end());
xv.erase(uniItr, xv.end());
map<int, int> index;
int idx = 0;
for (int i = 0; i < xv.size(); i++) {
index[xv[i]] = i;
}
vector<int> count(index.size());
vector<vector<int> > x;
int x1, x2, y1, y2;
for (int i = 0; i < v.size(); i++) {
x1 = v[i][0];
y1 = v[i][1];
x2 = v[i][2];
y2 = v[i][3];
x.push_back({ y1, x1, x2, 1 });
x.push_back({ y2, x1, x2, -1 });
}
sort(x.begin(), x.end());
lli ret = 0;
lli sum = 0, currentY = 0;
for (int i = 0; i < x.size(); i++) {
lli y = x[i][0];
x1 = x[i][1];
x2 = x[i][2];
int sig = x[i][3];
ret = add(ret, (y - currentY) * sum);
currentY = y;
for (int i = index[x1]; i < index[x2]; i++) {
count[i] += sig;
}
sum = 0;
for (int i = 0; i < count.size(); i++) {
if (count[i] > 0) {
sum += (xv[i + 1] - xv[i]);
}
}
}
return ret % m;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,0,2,2},{1,0,2,3},{1,0,3,1}};
cout << (ob.rectangleArea(v));
} ইনপুট
{{0,0,2,2},{1,0,2,3},{1,0,3,1}} আউটপুট
6


