ধরুন আমাদের একটি বাইনারি গাছ আছে; আমরা গাছের নোডগুলিতে ক্যামেরা রাখি। এখন একটি নোডে প্রতিটি ক্যামেরা তার পিতামাতা, নিজেকে এবং তার সন্তানদের নিরীক্ষণ করতে পারে। গাছের সমস্ত নোড নিরীক্ষণ করার জন্য আমাদের ন্যূনতম সংখ্যক ক্যামেরা খুঁজে বের করতে হবে।
সুতরাং, যদি ইনপুট −
এর মত হয়
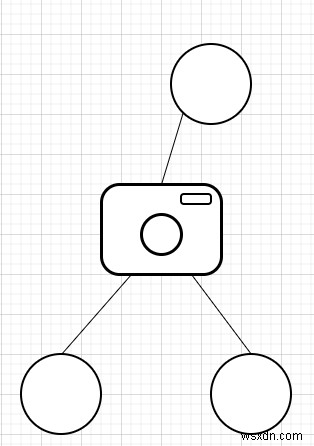
তাহলে আউটপুট হবে 1, কারণ সবগুলো ট্র্যাক করার জন্য শুধুমাত্র একটি ক্যামেরাই যথেষ্ট।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
আচ্ছাদিত নামক একটি সেট সংজ্ঞায়িত করুন, TreeNode প্রকারের (ট্রি নোডে বাম, ডান এবং ডেটা ক্ষেত্র রয়েছে)
-
একটি ফাংশন সংজ্ঞায়িত করুন সমাধান(), এটি নোড, প্যারেন্ট,
নেবে -
যদি নোড নাল হয়, তাহলে −
-
ফেরত
-
-
সমাধান (নোডের বামে, নোড)
-
সমাধান (নোডের ডান, নোড)
-
যদি (প্যারেন্ট NULL এর মতো এবং (নোড, নোডের বাম, নোডের ডানদিকে) কিছুই কভার না হয়, তাহলে -
-
(উত্তর 1 দ্বারা বৃদ্ধি করুন)
-
আচ্ছাদিত মধ্যে নোড ঢোকান
-
কভারে নোডের বাম দিকে ঢোকান
-
কভারে নোডের ডানদিকে সন্নিবেশ করুন
-
আবৃত মধ্যে অভিভাবক সন্নিবেশ করুন
-
-
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন,
-
উত্তর :=0
-
আচ্ছাদিত মধ্যে NULL ঢোকান
-
সমাধান (রুট, শূন্য)
-
উত্তর ফেরত দিন
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
class Solution {
public:
set<TreeNode*> covered;
int ans;
int minCameraCover(TreeNode* root){
covered.clear();
ans = 0;
covered.insert(NULL);
solve(root, NULL);
return ans;
}
void solve(TreeNode* node, TreeNode* parent){
if (!node)
return;
solve(node->left, node);
solve(node->right, node);
if ((parent == NULL && covered.find(node) == covered.end())
|| covered.find(node->left) == covered.end() || covered.find(node-
>right) == covered.end()) {
ans++;
covered.insert(node);
covered.insert(node->left);
covered.insert(node->right);
covered.insert(parent);
}
}
};
main(){
Solution ob;
TreeNode *root = new TreeNode(1);
root->left = new TreeNode(1);
root->left->left = new TreeNode(1); root->left->right = new
TreeNode(1);
cout << (ob.minCameraCover(root));
} ইনপুট
[1,1,NULL,1,1]
আউটপুট
1


