C++ এ 3n স্লাইস সহ পিৎজা

ধরুন বিভিন্ন আকারের 3n স্লাইস সহ একটি পিৎজা আছে, আমি এবং আমার দুই বন্ধু নিম্নরূপ পিজ্জার স্লাইস নেব −

আমি যেকোনো পিজ্জা স্লাইস বাছাই করব।
আমার বন্ধু অমল আমার বাছাইয়ের ঘড়ির কাঁটার বিপরীত দিকে পরবর্তী স্লাইস বেছে নেবে।
আমার বন্ধু বিমল আমার বাছাইয়ের ঘড়ির কাঁটার দিকে পরবর্তী স্লাইস বেছে নেবে।
পিজ্জার আর কোন স্লাইস না হওয়া পর্যন্ত এই পদক্ষেপগুলি পুনরাবৃত্তি করুন৷
৷

পিৎজা স্লাইসগুলির আকার ঘড়ির কাঁটার দিকে বৃত্তাকার অ্যারে স্লাইস দ্বারা প্রতিনিধিত্ব করা হয়। আমাদেরকে স্লাইস আকারের সর্বোচ্চ সম্ভাব্য যোগফল খুঁজে বের করতে হবে যা আমার কাছে থাকতে পারে।

সুতরাং, যদি ইনপুটটি [9,8,6,1,1,8],

এর মত হয়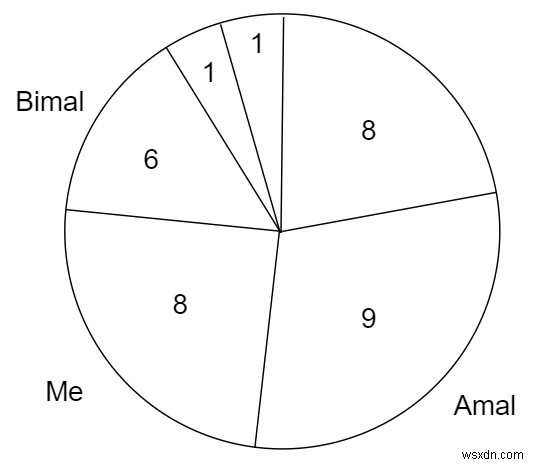

C++ এ 3n স্লাইস সহ পিৎজা

তারপর আউটপুট 16 হবে, প্রতিটি পালা করে 8 আকারের পিজা স্লাইস নিন। যদি আমি সাইজ 9 দিয়ে স্লাইস বাছাই করি আমার বন্ধুরা 8 সাইজের স্লাইস বাছাই করবে।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি ফাংশন সল্ভ() সংজ্ঞায়িত করুন, এটি একটি অ্যারে v, এবং একটি আর্গুমেন্ট m,

নেবে

n :=v
এর আকার
দুটি 2D অ্যারে dp1 এবং dp2 আকারের (n + 1) x (m + 1) প্রতিটি সংজ্ঞায়িত করুন
আরম্ভ করার জন্য i :=0, যখন i
- j শুরু করার জন্য :=0, যখন j <=m, আপডেট করুন (j 1 দ্বারা বৃদ্ধি করুন), −
  - x :=v[i]
  - যদি j
    - dp2[i + 1, j + 1] =সর্বাধিক dp2[i + 1, j + 1] এবং dp1[i, j] + x)
    - dp1[i + 1, j] =সর্বাধিক dp1[i + 1, j], dp2[i, j] এবং dp1[i, j]
সর্বোচ্চ dp1[n, m] এবং dp2[n, m]
ফেরত দিন
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
n :=স্লাইসের আকার
ret :=0
ret :=সমাধানের সর্বাধিক (সূচী 1 থেকে শেষ পর্যন্ত স্লাইস, n/3) এবং স্লাইস[0] + সমাধান (সূচি 2 থেকে শেষ পর্যন্ত - 1, n/3 - 1)
রিটার্ন রিটার্ন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

#include <bits/stdc++.h>
using namespace std;
class Solution {
   public:
   int solve(vector <int> v, int m){
      int n = v.size();
      vector<vector<int> > dp1(n + 1, vector<int>(m + 1));
      vector<vector<int> > dp2(n + 1, vector<int>(m + 1));
      for (int i = 0; i < n; i++) {
         for (int j = 0; j <= m; j++) {
            int x = v[i];
            if (j < m)
            dp2[i + 1][j + 1] = max(dp2[i + 1][j + 1], dp1[i]
            [j] + x);
            dp1[i + 1][j] = max({ dp1[i + 1][j], dp2[i][j],
            dp1[i][j] });
         }
      }
      return max(dp1[n][m], dp2[n][m]);
   }
   int maxSizeSlices(vector<int>& slices) {
      int n = slices.size();
      int ret = 0;
      ret = max(solve(vector<int>(slices.begin() + 1,
      slices.end()), n / 3), slices[0] + solve(vector<int>(slices.begin() +
      2, slices.end() - 1), n / 3 - 1));
      return ret;
   }
};
main(){
   Solution ob;
   vector<int> v = {9,8,6,1,1,8};
   cout << (ob.maxSizeSlices(v));
}

ইনপুট

{9,8,6,1,1,8}