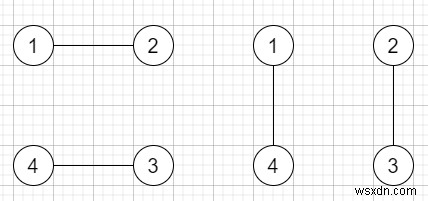
হ্যান্ডশেক যা C++ এ অতিক্রম করে না

ধরুন আমাদের কাছে একটি জোড় সংখ্যক লোক আছে যারা একটি বৃত্তের চারপাশে দাঁড়িয়ে আছে এবং প্রত্যেক ব্যক্তি অন্য কারো সাথে হ্যান্ডশেক করছে, যাতে মোট n/2টি হ্যান্ডশেক হবে। এই হ্যান্ডশেকগুলি এমনভাবে ঘটতে পারে যে হ্যান্ডশেকগুলির কোনওটিই ক্রস না হয় তার সংখ্যা আমাদের খুঁজে বের করতে হবে। উত্তরগুলি অনেক বড় হতে পারে তাই উত্তর মোড 10^9 + 7 ফেরত দিন।

সুতরাং, যদি ইনপুট n =2 এর মত হয়, তাহলে আউটপুট হবে 1

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

m :=10^9 + 7
আকারের একটি অ্যারে ডিপি সংজ্ঞায়িত করুন (n+1)
dp[0] :=1
আরম্ভ করার জন্য i :=0, যখন i <=n, আপডেট i :=i + 2, do −
- j শুরু করার জন্য :=0, যখন j <=i-2, আপডেট j :=j + 2, do −
  - dp[i] :=dp[i] + (dp[j] mod m * dp[i - 2 - j] mod m)
  - dp[i] :=dp[i] mod m
dp[n] mod m
ফেরত দিন

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

উদাহরণ

#include <bits/stdc++.h>
using namespace std;
const int m = 1e9+7;
typedef long long int lli;
class Solution {
   public:
   int numberOfWays(int n) {
      vector <lli> dp(n+1);
      dp[0] = 1;
      for(int i = 0; i <= n; i+=2 ){
         for(int j =0 ; j <= i-2; j+=2){
            dp[i] += (dp[j]%m * dp[i-2-j]%m)%m;
            dp[i]%=m;
         }
      }
      return dp[n]%m;
   }
};
main(){
   Solution ob;
   cout << (ob.numberOfWays(2));
}