আমাদের একটি বাইনারি গাছের উচ্চতা H দেওয়া হয়েছে। লক্ষ্য হল প্রদত্ত উচ্চতার সুষম বাইনারি গাছের সংখ্যা/গণনা খুঁজে বের করা।
একটি বাইনারি গাছ − হল একটি ট্রি ডেটা স্ট্রাকচার যেখানে প্রতিটি নোডে সর্বাধিক দুটি শিশু থাকে, যা বাম শিশু এবং ডান শিশু।
উচ্চতা-ভারসাম্যপূর্ণ বাইনারি গাছ − একটি বাইনারি ট্রি হিসাবে সংজ্ঞায়িত করা হয় যেখানে প্রতিটি নোডের দুটি উপবৃক্ষের গভীরতা শুধুমাত্র 1 বা 0 দ্বারা পৃথক হয়। এটি হল বাম সাবট্রির উচ্চতা এবং প্রতিটি নোডে ডান সাবট্রির সর্বোচ্চ পার্থক্য 1।
নিম্নোক্ত চিত্রটিতে উচ্চতা h=3.
এর জন্য সম্ভাব্য উচ্চতা সুষম বাইনারি গাছ রয়েছে
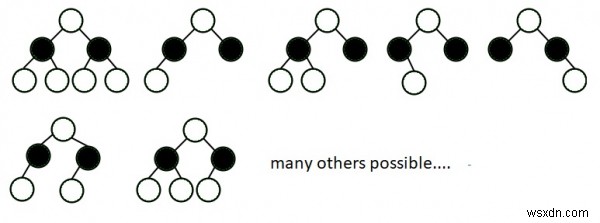
ইনপুট
Height H=2
আউটপুট
Count of Balanced Binary Trees of Height H is : 3
ব্যাখ্যা - প্রদত্ত চিত্রে উচ্চতা H=2
এর জন্য সম্ভাব্য সুষম গাছ রয়েছে

ইনপুট
Height H=3
আউটপুট
Count of Balanced Binary Trees of Height H is : 15
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি
-
পূর্ণসংখ্যা H ব্যবহার করা হয় বাইনারি গাছের উচ্চতা বোঝাতে।
-
কাউন্টBTheight(int h) ফাংশনটি গাছের উচ্চতাকে ইনপুট হিসেবে নেয় এবং উচ্চতা h সহ সম্ভাব্য ব্যালেন্সড বাইনারি গাছের সংখ্যা প্রদান করে।
-
আমরা পুনরাবৃত্ত পদ্ধতি ব্যবহার করছি।
-
যদি গাছটির উচ্চতা 1 থাকে, অর্থাৎ এটির শুধুমাত্র একটি নোড থাকে তবে একটি একক নোড সহ শুধুমাত্র একটি গাছ উপস্থিত থাকে এবং এটি সুষম। ( if(h==1), রিটার্ন 1)
-
অন্যথায় উচ্চতা হল বাম ও ডান উপবৃক্ষের সমষ্টি যার উচ্চতা মূলের চেয়ে এক বা দুই কম। (সুষম গাছের উচ্চতার মধ্যে 1 হিসাবে পার্থক্য রয়েছে)।
-
ফাংশন ফলাফল হিসাবে গণনা প্রদান করে।
উদাহরণ
#include <iostream>
int countBTheight(int h){
// One tree is possible with height 0 or 1
if (h == 0 || h == 1)
return 1;
return countBTheight(h-1) * (2 *countBTheight(h-2) + countBTheight(h-1));
}
int main(){
int H = 4;
std::cout << "Count of balanced binary trees of height H is: "<<countBTheight(H);
} আউটপুট
Count of balanced binary trees of height H is: 315


