ইনপুট হিসেবে আমাদের দুটি বাইনারি সার্চ ট্রি এবং একটি ভেরিয়েবল x দেওয়া হয়েছে। লক্ষ্য হল প্রতিটি গাছ থেকে নোডের জোড়া খুঁজে বের করা যাতে নোডের মানের সমষ্টি x এর সমান হয়। BST_1 থেকে নোড 1 এবং BST_2 থেকে নোড 2 নিন এবং উভয়ের ডেটা অংশ যোগ করুন। যোগফল=x হলে। সংখ্যা বৃদ্ধি।
আসুন উদাহরণ দিয়ে বুঝতে পারি।
ইনপুট
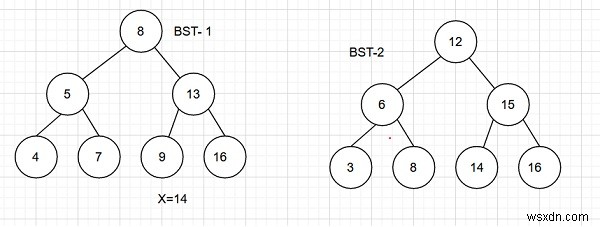
আউটপুট − দুটি BST থেকে জোড়ার সংখ্যা যার যোগফল একটি প্রদত্ত মানের x এর সমান - 1
ব্যাখ্যা − জোড়া হল (8,6)
ইনপুট
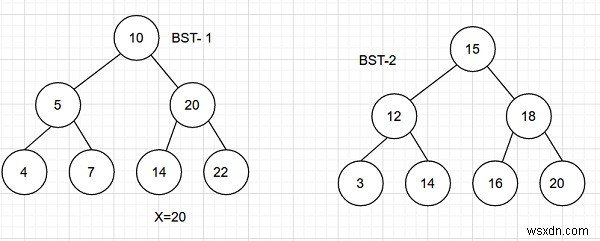
আউটপুট −দুটি BST থেকে জোড়ার সংখ্যা যার যোগফল একটি প্রদত্ত মানের x এর সমান − 2
ব্যাখ্যা − জোড়া হল (5,15) এবং (4,16)
নিচের প্রোগ্রামে ব্যবহৃত পদ্ধতিটি নিম্নরূপ
এই পদ্ধতিতে আমরা একটি পুনরাবৃত্তিমূলক ইনঅর্ডার পদ্ধতি ব্যবহার করে BST-এর পথ অতিক্রম করব। পুনরাবৃত্তিমূলক ইনঅর্ডার পদ্ধতি ব্যবহার করে ক্ষুদ্রতম নোড থেকে সবচেয়ে বড় নোড থেকে বিএসটি 1 অতিক্রম করুন এবং পুনরাবৃত্তিমূলক ইনঅর্ডার পদ্ধতির বিপরীত থেকে বিএসটি 2 অতিক্রম করুন। উভয় BST এর বর্তমান নোডের যোগফল নিন। যোগফল x বৃদ্ধির গণনা হলে। যদি sum>x হয় তাহলে BST 2-এ বর্তমান নোডের পূর্বসূরিতে যান। যদি যোগফল
দুটি গাছ নিন BST_1 এবং BST_2 যাতে পূর্ণসংখ্যার ডেটা অংশ থাকে এবং বাম, ডানদিকে চাইল্ড নোডের নির্দেশক থাকে।
ফাংশন insert_node(int data) ডাটা সহ ট্রিতে একটি নতুন নোড সন্নিবেশ করায় এবং এতে একটি পয়েন্টার ফেরত দেয়।
inser_node() ব্যবহার করে উভয় BST তৈরি করুন এবং BST_sum_x(Tree* BST_1, Tree* BST_2, int x) এ পাস করুন।
ফাংশন BST_sum_x(Tree* BST_1, Tree* BST_2, int x) উভয় গাছের রুট নোড নেয় এবং x হিসাবে ডেটা অংশের সমষ্টি সহ নোডের জোড়ার গণনা প্রদান করে।
যোগফল x সহ জোড়ার সংখ্যার জন্য 0 হিসাবে প্রাথমিক গণনা নিন।
পুনরাবৃত্তিমূলক ইনঅর্ডার ট্রাভার্সালের জন্য দুটি ভেরিয়েবল নিন Tree* stack_top_1, *stack_top_2;
দুটি স্ট্যাক তৈরি করুন স্ট্যাক স্ট্যাক_1, স্ট্যাক_2;
এখন লুপ থাকার সময় বাইরে শুরু করুন৷
যখন লুপ ব্যবহার করে BST_1 এর বামদিকের (সবচেয়ে ছোট) নোডে যান এবং সমস্ত নোডকে স্ট্যাক_1 এ ঠেলে দিন
যখন লুপ ব্যবহার করে BST_2 এর ডানদিকের (সর্বশ্রেষ্ঠ) নোডে যান এবং সমস্ত নোডকে স্ট্যাক_2 এ ঠেলে দিন
যদি কোন স্ট্যাক খালি থাকে তবে লুপ করার সময় বাইরের অংশটি ভেঙে দিন।
উভয় স্ট্যাকের শীর্ষ নোড নিন এবং তাদের ডেটা অংশ যোগ করুন এবং টেম্পে সংরক্ষণ করুন।
যদি temp ( যোগফল) ==x হয় তাহলে ইনক্রিমেন্ট গণনা। পপ অপারেশন ব্যবহার করে স্ট্যাক_1 এবং স্ট্যাক_2 উভয় থেকে শীর্ষ উপাদানগুলি সরান৷
BST_1=stack_1->ডান এবং BST_2=stack_2->বাম সেট করুন ( BST_1-এ পরবর্তী উত্তরসূরী এবং BST_2-এ পূর্বসূরি)
যদি temp
IF temp>
x তারপর শুধুমাত্র স্ট্যাক_2 থেকে শীর্ষ সরান এবং BST_1-এ পরবর্তী পূর্বসূরিতে যান।
বাইরের সময় শেষে, উভয় BST-এর নোডের সমষ্টি x সহ গণনার সংখ্যায় জোড়া রয়েছে।
ফলাফল হিসাবে রিটার্ন গণনা।
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট −
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
struct Tree{
int data;
Tree* left, *right;
};
Tree* insert_node(int data){
Tree* newNode = (Tree*)malloc(sizeof(Tree));
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
}
int BST_sum_x(Tree* BST_1, Tree* BST_2, int x){
int count = 0;
Tree* stack_top_1, *stack_top_2;
stack<Tree*> stack_1, stack_2;
if (BST_1 == NULL || BST_2 == NULL){
return 0;
}
while (1){
while (BST_1 != NULL){
stack_1.push(BST_1);
BST_1 = BST_1->left;
}
while (BST_2 != NULL){
stack_2.push(BST_2);
BST_2 = BST_2->right;
}
if (stack_1.empty() || stack_2.empty()){
break;
}
stack_top_1 = stack_1.top();
stack_top_2 = stack_2.top();
int temp = stack_top_1->data + stack_top_2->data;
if (temp == x){
count++;
stack_1.pop();
stack_2.pop();
BST_1 = stack_top_1->right;
BST_2 = stack_top_2->left;
}
else if (temp < x){
stack_1.pop();
BST_1 = stack_top_1->right;
}
else{
stack_2.pop();
BST_2 = stack_top_2->left;
}
}
return count;
}
int main(){
//BST 1
Tree* BST_1 = insert_node(15);
BST_1->left = insert_node(10);
BST_1->right = insert_node(8);
BST_1->left->left = insert_node(12);
BST_1->left->right = insert_node(24);
BST_1->right->left = insert_node(16);
//BST 2
Tree* BST_2 = insert_node(20);
BST_2->left = insert_node(16);
BST_2->right = insert_node(4);
BST_2->left->left = insert_node(18);
BST_2->left->right = insert_node(28);
BST_2->right->left = insert_node(22);
int x = 28;
cout<<"Count of pairs from two BSTs whose sum is equal to a given value x ar: "<<BST_sum_x(BST_1, BST_2, x);
return 0;
} আউটপুট
Count of pairs from two BSTs whose sum is equal to a given value x ar: 1


