আমাদেরকে এর পরিধিতে K সমদূরবর্তী বিন্দু সহ একটি বৃত্ত দেওয়া হয়েছে। এছাড়াও আমাদের দুটি বিন্দু A এবং B দেওয়া হয়েছে। লক্ষ্য হল এই বিন্দুগুলি ব্যবহার করে সম্ভাব্য ত্রিভুজের সংখ্যা গণনা করা যাতে তাদের ভিতরে একটি স্থূলকোণ ACB (90o-এর বেশি কোণ) থাকে। বিন্দু A এবং B এমন যে A
এখানে K=8, A=2, B=5, বিন্দুর সংখ্যা=2 (C,C’) যেমন কোণ LACB, LAC’B স্থূল।
আসুন উদাহরণ দিয়ে বুঝতে পারি
ইনপুট − k=10, A=2, B=4
আউটপুট − 2টি প্রদত্ত বিন্দুর মধ্যে 'k' সমদূরত্ব বিন্দু সহ একটি বৃত্তে স্থূলকোণগুলির গণনা হল − 1
ব্যাখ্যা − বিন্দু হবে C=3
ইনপুট − k=12, A=2, B=10
আউটপুট − 2টি প্রদত্ত বিন্দুর মধ্যে 'k' সমদূরত্ব বিন্দু সহ একটি বৃত্তে স্থূলকোণগুলির গণনা হল −3
এটি দেখা যায় যে A এবং B এর মধ্যে চাপটি যত ছোট হবে বিন্দুগুলি কেবল সেই চাপের উপর থাকবে।
উভয় চাপ গণনা করুন এবং যদি সেগুলি সমান দৈর্ঘ্যের হয় তবে এমন কোন ত্রিভুজ সম্ভব নয়, 0 ফেরত দিন। অন্যথায় বিন্দুর পরিপ্রেক্ষিতে দূরত্বকে ছোট চাপ হিসাবে গণনা সেট করুন।
k, point_a এবং point_b.
ফাংশন Obtuse_angle_circle(int point_a, int point_b, int k) সমস্ত ভেরিয়েবল নেয় এবং 2টি প্রদত্ত বিন্দুর মধ্যে 'k' সমদূরত্ব বিন্দু সহ একটি বৃত্তে স্থূলকোণগুলির গণনা প্রদান করে
0 হিসাবে প্রাথমিক গণনা নিন।
প্রথম চাপটিকে arc_1 =(বিন্দু_বি - পয়েন্ট_এ) - 1 হিসাবে গণনা করুন। (b>a)
দ্বিতীয় চাপটি (k - point_b) + (point_a - 1) হিসাবে গণনা করুন।
যদি উভয় আর্ক সমান হয় তাহলে 0 ফেরত দিন কারণ এইরকম কোন বিন্দু সম্ভব নয়।
যদি সেগুলি অসম হয় তাহলে ন্যূনতম দুটি হিসাবে আপডেট করুন কারণ সমস্ত পয়েন্ট এতে রয়েছে৷
ফলাফল হিসাবে রিটার্ন গণনা।
যদি আমরা উপরের কোডটি চালাই তবে এটি নিম্নলিখিত আউটপুট −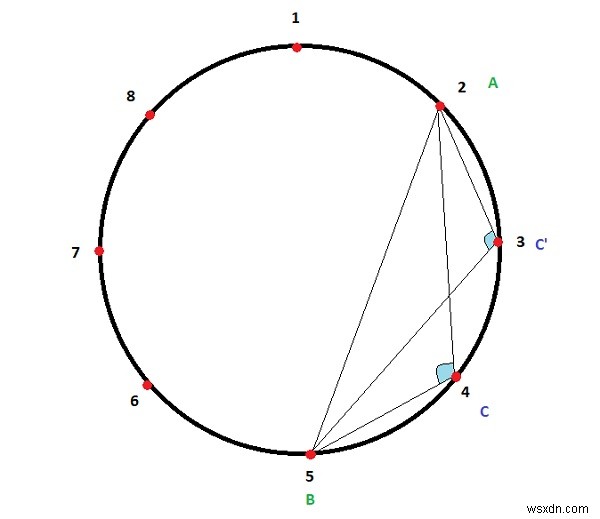
নিম্নলিখিত প্রোগ্রামে ব্যবহৃত পদ্ধতি
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
int Obtuse_angle_circle(int point_a, int point_b, int k){
int count = 0;
int arc_1 = (point_b - point_a) - 1;
int arc_2 = (k - point_b) + (point_a - 1);
if (arc_1 == arc_2){
return 0;
}
count = min(arc_1, arc_2);
return count;
}
int main(){
int k = 10;
int point_a= 1;
int point_b = 4;
cout<<"Count of obtuse angles in a circle with ‘k' equidistant points between 2 given pointsare: "<<Obtuse_angle_circle(point_a, point_b, k);
return 0;
} আউটপুট
Count of obtuse angles in a circle with ‘k' equidistant points between 2 given points are: 2


